М. Бабаев - Гидравлика
- Название:Гидравлика
- Автор:
- Жанр:
- Издательство:Конспекты, шпаргалки, учебники «ЭКСМО»b4455b31-6e46-102c-b0cc-edc40df1930e
- Год:2008
- Город:Москва
- ISBN:978-5-699-24848-3
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
М. Бабаев - Гидравлика краткое содержание
Введите сюда краткую аннотацию
Гидравлика - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:

где N – половина экстремума вне кривой мгновенных скоростей;
Т – период осреднения;
T/N = 1/w– период пульсации.
39. Распределение скоростей при равномерном установившемся движении. Ламинарная пленка
Все же, несмотря на вышеперечисленные и другие особенности, о которых не сказано из-за их невостребованности, основным признаком турбулентного движения является перемешивание частиц жидкости.
Принято об этом перемешивании с точки зрения количества говорить как о перемешивании молей жидкости.
Как мы убедились выше, с ростом числа Re интенсивность турбулентности нe растет. Несмотря на это, все же, например, у внутренней поверхности трубы (или у любой другой твердой стенки) существует некоторый слой, в пределах которого все скорости, в том числе пульсационные «добавки», равны нулю: это очень интересное явление.
Этот слой принято называть вязким подслоем потока.
Само собой на границе соприкосновения с основной массой потока этот вязкий подслой все же имеет некоторую скорость. Следовательно, все изменения в основном потоке передаются и в подвязкий слой, но их значение очень мало. Это позволяет считать движение слоя ламинарным.
Ранее, считая, что эти передачи в подвязкий слой отсутствуют, слой назвали ламинарной пленкой. Теперь нетрудно убедиться, что с точки зрения современной гидравлики ламинарность движения в этом слое относительная (интенсивность ε в подвязком слое (ламинарной пленке) может достигать значения 0,3. Для ламинарного движения это достаточно большая величина)
Подвязкий слой ε вочень тонкий по сравнению с основным потоком. Именно наличие этого слоя порождает потери напора (удельной энергии).
Что касается толщины ламинарной пленки δ в, то она обратно пропорциональна числу Re. Это более наглядно видно из следующего сравнения толщины в зонах потока при турбулентном движении.
Вязкий (ламинарный) слой – 0 < ua / V < 7.
Переходная зона – 7 < ua/V < 70.
Турбулентное ядро – ua/V < 70.
В этих соотношениях u – динамическая скорость потока, а – расстояние от твердой стенки, V – кинематическая вязкость.
Углубимся немного в историю теории турбулентности: эта теория включает в себя совокупность гипотез, на основании которых были получены зависимости между основными параметрами u i,τ турбулентного движения потока.
У разных исследователей к этому вопросу были разные подходы. Среди них немецкий ученый Л. Прандтль, советский ученый Л. Ландау и многие другие.
Если до начала XX в. ламинарный слой, по мнению ученых, представлял собой некоторый мертвый слой, в переходе к которому (или от которого) происходит как бы разрыв скоростей, то есть скорость меняется скачкообразно, то в современной гидравлике совсем другая точка зрения.
Поток – это «живое» явление: все переходные процессы в нем носят непрерывный характер.
40. Распределение скоростей в «живом» сечении потока
Современной гидродинамике удалось разрешить эти проблемы, применив метод статистического анализа. Основным орудием этого метода является то, что исследователь выходит за рамки традиционных подходов и применяет для анализа некие средние по времени характеристики потока.
Усредненная скорость
Ясно, что в любой точке живого сечения любую мгновенную скорость и можно разложить на u x, u y, u zкомпоненты.
Мгновенная скорость определяется по формуле:
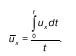
Полученную скорость можно назвать скоростью, усредненной по времени, или средней местной эта скорость u x– фиктивно постоянная и позволяет судить о характеристике потока.
Вычислив u y,u xможно получить вектор усредненной скорости
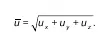
Касательные напряжения τ = τ + τ ,
определим и суммарное значение касательного напряжения τ. Поскольку это напряжение возникает из-за наличия сил внутреннего трения, то жидкость считают ньютоновой.
Если предположить, что площадь соприкосновения – единичная, то сила сопротивления
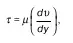
где μ – динамическая вязкость жидкости;
dυ/dy – изменение скорости. Эту величину часто называют градиентом скорости, или скоростью сдвига.
В настоящее время руководствуются выражением, полученным в вышеупомянутом уравнении Прандтля:
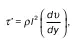
где ρ– плотность жидкости;
l– длина пути, на котором рассматривается движение.
Без вывода приводим окончательную формулу для пульсационной «добавки» касательного напряжения:
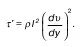
42. Параметры потока, от которых зависит потеря напора. Метод размерностей
Неизвестный вид зависимости определяется по методу размерностей. Для этого существует π-теорема: если некоторая физическая закономерность выражена уравнением, содержащим к размерных величин, причем оно содержит п величин с независимой размерностью, то это уравнение может быть преобразовано в уравнение, содержащее (к-п) независимых, но уже безразмерных комплексов.
Для чего определимся: от чего зависят потери напора при установившемся движении в поле сил тяжести.
Эти параметры.
1. Геометрические размеры потока:
1) характерные размеры живого сечения l 1l 2;
2) длина рассматриваемого участка l;
3) углы, которыми завершается живое сечение;
4) свойства шероховатости: Δ– высота выступа и lΔ – характер продольного размера выступа шероховатости.
2. Физические свойства:
1) ρ – плотность;
2) μ – динамическая вязкость жидкости;
3) δ – сила поверхностного натяжения;
4) Е ж– модуль упругости.
3. Степень интенсивности турбулентности, характеристикой которой является среднеквадратичное значение пульсационных составляющих δu.
Теперь применим π-теорему.
Исходя из приведенных выше параметров, у нас набирается 10 различных величин:
l, l 2, Δ, l Δ, Δp, μ, δ, E ж,δ u, t.
Кроме этих, имеем еще три независимых параметра: l 1, ρ, υ. Добавим еще ускорение падения g.
Всего имеем к = 14 размерных величин, три из которых независимы.
Требуется получить (ккп) безразмерных комплексов, или, как их называют π-членов.
Для этого любой параметр из 11, который не входил бы в состав независимых параметров (в данном случае l 1, ρ, υ), обозначим как N i, теперь можно определить безразмерный комплекс, который является характеристикой этого параметра N i, то есть i-тый π-член:
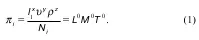
Здесь углы размерности базовых величин:
Читать дальшеИнтервал:
Закладка:






