М. Бабаев - Гидравлика
- Название:Гидравлика
- Автор:
- Жанр:
- Издательство:Конспекты, шпаргалки, учебники «ЭКСМО»b4455b31-6e46-102c-b0cc-edc40df1930e
- Год:2008
- Город:Москва
- ISBN:978-5-699-24848-3
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
М. Бабаев - Гидравлика краткое содержание
Введите сюда краткую аннотацию
Гидравлика - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:

где χ – смоченный периметр,
w – площадь живого сечения,
l he– длина пути потока,
ρ, g – плотность жидкости и ускорение силы тяжести,
τ 0– касательное напряжение вблизи внутренних стенок трубы.
Следует:

Откуда с учетом
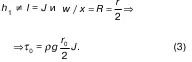
Исходя из полученных результатов для τ 0, распределения касательного напряжения τ в произвольно выбранной точке выделенного объема, например, в точке r 0– r = t это расстояние равно:

тем самым вводим касательное напряжение t на поверхности цилиндра, действующее на точку в r 0– r= t.
Из сравнений (4) и (3) следует:
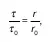
поэтому

Подставив r= r 0– t в (5), получим

Выводы:
1) при равномерном движении распределение касательного напряжения по радиусу трубы подчиняется линейному закону;
2) на стенке трубы касательное напряжение максимально (когда r 0= r, т. е. t = 0), на оси трубы оно равно нулю (когда r 0= t).
R– гидравлический радиус трубы, получим, что

47. Турбулентный равномерный режим движения потока
Если рассмотреть плоское движение (т. е. потенциальное движение, когда траектории всех частиц параллельны одной и той же плоскости и являются функции ей двух координат и если движение неустановившееся), одновременно являющееся равномерным турбулентным в системе координат XYZ, когда линии тока параллельны оси OX, то
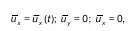
Усредненная скорость при сильно турбулентном движении.
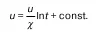
Это выражение: логарифмический закон распределения скоростей для турбулентного движения.
При напорном движении поток состоит в основном из пяти областей:
1) ламинарная: приосевая область, где местная скорость максимальна, в этой области λ лам= f(Re), где число Рейнольдса Re < 2300;
2) во второй области поток начинает переходить из ламинарного в турбулентный, следовательно, увеличивается и число Re;
3) здесь поток полностью турбулентный; в этой области трубы называются гидравлическими гладкими (шероховатость Δ меньше, чем толщина вязкого слоя δ в, то есть Δ < δ в).
В случае, когда Δ> δ в, труба считается «гидравлически шероховатой».
Характерно, что если для λ лам= f(Re –1), то в этом случае λ гд= f(Re – 0,25);
4) эта область находится на пути перехода потока к подвязкому слою: в этой области λ лам= (Re, Δ/r0). Как видно, коэффициент Дарси уже начинает зависеть от абсолютной шероховатости Δ;
5) эта область называется квадратичной областью (коэффициент Дарси не зависит от числа Рейнольдса, но определяется почти полностью касательным напряжением) и является пристенной.
Эту область называют автомодельной, т. е. не зависящей от Re.
В общем случае, как известно, коэффициент Шези
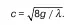
Формула Павловского:

где п – коэффициент шероховатости;
R– гидравлический радиус.
При 0,1 ≤ R ≤ 3 м
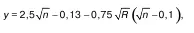
причем при R< 1 м
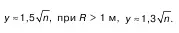
48. Неравномерное движение: формула Вейсбаха и ее применение
При равномерном движении потери напора, как правило, выражаются формулой

где потери напора h прзависят от скорости потока; она постоянна, поскольку, движение равномерное.
Следовательно, и формула (1) имеет соответствующие формы.
Действительно, если в первом случае

то во втором случае

Как видно, формулы (2) и (3) различаются только коэффициентом сопротивления x.
Формула (3) называется формулой Вейсбаха. В обоих формулах, как и в (1), коэффициент сопротивления – величина безразмерная, и в практических целях определяется, как правило, по таблицам.
Для проведения опыта по определению xм последовательность действий следующая:
1) должен быть обеспечен ход равномерности потока в исследуемом конструктивном элементе. Необходимо обеспечить достаточное удаление от входа пьезометров.
2) для установившегося движения вязкой несжимаемой жидкости между двумя сечениями (в нашем случае, это вход с x 1υ 1и выход с x 2υ 2), применяем уравнение Бернулли:
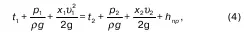
В рассматриваемых сечениях поток должен быть плавно изменяющимся. Между сечениями могло бы произойти что угодно.
Поскольку суммарные потери напора

то находим потери напора на этом же участке;
3) по формуле (5) находим, что h м= h пр– h l, после этого по формуле (2) находим искомый коэффициент
сопротивления

49. Местные сопротивления
Что происходит после того, как поток вошел с некоторым напором и скоростью в трубопровод.
Это зависит от вида движения: если поток ламинарный, то есть его движение описывается линейным законом, тогда его кривая – парабола. Потери напора при таком движении достигают (0,2 × 0,4) × (υ 2/ 2g).
Читать дальшеИнтервал:
Закладка:






