М. Бабаев - Гидравлика
- Название:Гидравлика
- Автор:
- Жанр:
- Издательство:Конспекты, шпаргалки, учебники «ЭКСМО»b4455b31-6e46-102c-b0cc-edc40df1930e
- Год:2008
- Город:Москва
- ISBN:978-5-699-24848-3
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
М. Бабаев - Гидравлика краткое содержание
Введите сюда краткую аннотацию
Гидравлика - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
В результате растяжки трубы произойдет приращение радиуса трубы на Δr, то есть радиус станет равным r= r 0+ Δr. Из-за этого увеличится круглое сечение поперечного сечения на Δω = ω– ω 0. Все это приведет к приращению объема на
ΔV 1= (ω– ω 0)Δl = ΔωΔl. (3)
Следует иметь в виду, что индекс ноль означает принадлежность параметра к начальному состоянию.
Что касается жидкости, то ее объем уменьшится на ΔV 2из-за приращения давления на Δp.
Искомая формула скорости распространения волны гидравлического удара
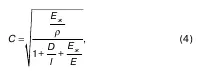
где ρ– плотность жидкости;
D/l – параметр, характеризующий толщину стенки трубы.
Очевидно, что чем больше D/l, тем меньше скорость распространения волны С. Если труба жесткая абсолютно, то есть Е = ∞, то, как следует из (4)

53. Дифференциальные уравнения неустановившегося движения
Для того, чтобы составить уравнение любого вида движения, нужно проецировать все действующие силы на систему и приравнивать их сумму к нулю. Так и поступим.
Пусть имеем напорный трубопровод круглого сечения, в котором есть неустановившееся движение жидкости.
Ось потока совпадает с осью l. Если выделить на этой оси элемент dl, то, согласно вышеуказанному правилу, можно составить уравнение движения
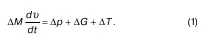
В приведенном уравнении проекции четырех сил, действующих на поток, точнее, на Δl, равны нулю:
1) ΔM – силы инерции, действующие на элемент dl;
2) Δp – силы гидродинамического давления;
3) ΔT – касательные силы;
4) ΔG – силы тяжести: здесь мы, говоря о силах, имели в виду проекции сил, действующих на элемент Δl.
Перейдем к формуле (1), непосредственно к проекциям действующих сил на элемент Δt, на ось движения.
1. Проекции поверхностных сил:
1) для гидродинамических сил Δp проекцией будет

2) для касательных сил ΔT
Проекция касательных сил имеет вид:
–ρgωJdl. (3)
2. Проекция сил тяжести Δ ΔG на элемент Δ Δ
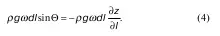
3. Проекция сил инерции Δ ΔM равна
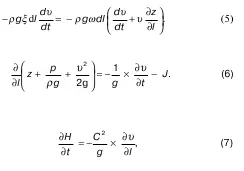
54. Истечение жидкости при постоянном напоре через малое отверстие
Будем рассматривать истечение, которое происходит через малое незатопленное отверстие. Для того, чтобы отверстие считать малым, должны выполняться условия:
1) напор в центре тяжести Н >> d, где d – высота отверстия;
2) напор в любой точке отверстия практически равен напору в центре тяжести Н.
Что касается затопленности, то таковой считают истечение под уровень жидкости при условии, если не изменяются со временем: положение свободных поверхностей до и после отверстий, давление на свободные поверхности до и после отверстий, атмосферное давление по обе стороны от отверстий.
Таким образом, имеем резервуар с жидкостью, у которой плотность ρ, из которого через малое отверстие происходит истечение под уровень. Напор Н в центре тяжести отверстия постоянен, что значит, скорости истечения постоянны. Следовательно, движение установившееся. Условием равенства скоростей на противоположных вертикальных границах отверстий является условие d ≤ 0,1Н, где d – наибольший вертикальный размер.
Ясно, что нашей задачей является определение скорости истечения и расхода жидкости в нем.
Сечение струи, отстоящее от внутренней стенки резервуара на расстояние 0,5d, называют сжатым сечением струи, которое характеризуется коэффициентом сжатия
Формулы определения скорости и расхода потока:
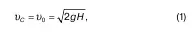
где υ 0называется коэффициентом скорости.
Теперь выполним вторую задачу, определим расход Q. По определению
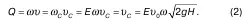
Обозначим Еυ 0= μ 0, где μ 0– коэффициент расхода, тогда
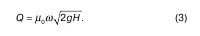
Различают следующие разновидности сжатия:
1. Полное сжатие – это такое сжатие, которое происходит по всему периметру отверстия, в противном случае сжатие считается неполным сжатием.
2. Совершенное сжатие является одной из двух разновидностей полного сжатия. Это такое сжатие, когда кривизны траектории, следовательно, и степень сжатия струи наибольшие.
Подводя итог, заметим, что неполная и несовершенная формы сжатий приводят к росту коэффициента сжатия. Характерной особенностью совершенного сжатияявляется то, что в зависимости от того, под воздействием каких сил происходит истечение.
55. Истечение через большое отверстие
Отверстие считают малым, когда его вертикальные размеры d < 0,1Н. Большим отверстием будем считать такое отверстие, для которого тот же d> 0,1Н.
Рассматривая истечение через малое отверстие, практически пренебрегли различием скоростей в разных точках сечения струи. В этом случае поступить так же мы не сможем.
Задача та же: определить расход и скорости в сжатом сечении.
Поэтому расход определяют следующим способом: выделяют бесконечно малую горизонтальную высоту dz. Таким образом, получается горизонтальная полоса с переменной длиной bz. Тогда, интегрировав по длине, можно найти элементарный расход
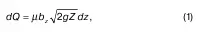
где Z – переменный напор по высоте отверстия, на такую глубину погружен верх выбранной полосы;
μ – коэффициент расхода через отверстие;
b z– переменная длина (или ширина) полосы.
Расход Q (1) можем определить, если μ = const и известна формула b z= f(z). В общем случае, расход определяют по формуле
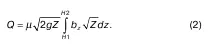
Если форма отверстия прямоугольная, то bz= b = const, интегрировав (2), получаем:
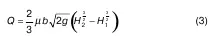
где Н 1, Н 2– напоры на уровнях соответственно у верхней и у нижней кромок отверстия;
Читать дальшеИнтервал:
Закладка:






