М. Бабаев - Гидравлика
- Название:Гидравлика
- Автор:
- Жанр:
- Издательство:Конспекты, шпаргалки, учебники «ЭКСМО»b4455b31-6e46-102c-b0cc-edc40df1930e
- Год:2008
- Город:Москва
- ISBN:978-5-699-24848-3
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
М. Бабаев - Гидравлика краткое содержание
Введите сюда краткую аннотацию
Гидравлика - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
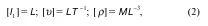
общий вид зависимости для всех 14 параметров имеет вид:
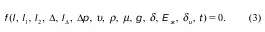
43. Равномерное движение и коэффициент сопротивления по длине. Формула Шези. Средняя скорость и расход потока
При ламинарном движении (если оно равномерное) ни живое сечение, ни средняя скорость, ни эпюра скоростей по длине не меняются со временем.
При равномерном движении пьезометрический уклон
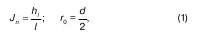
где l 1– длина потока;
h l– потери напора на длине L;
r 0d – соответственно радиус и диаметр трубы.

В формуле (2) безразмерный коэффициент λ называют коэффициентом гидравлического трения или коэффициентом Дарси.
Если в (2) d заменить на гидравлический радиус, то следует
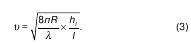
Введем обозначение
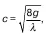
тогда с учетом того, что
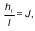
гидравлический уклон

Эту формулу называют формулой Шези.

называется коэффициентом Шези.
Если коэффициент Дарси λ – величина безразмерр
ная, то коэффициент Шези с имеет размерность

Определимся с расходом потока с участием коэфф
фициента Шези:
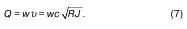
Преобразуем формулу Шези в следующий вид:
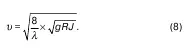
Величину
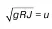
называют динамической скоростью
44. Гидравлическое подобие
Понятие о подобии. Гидродинамическое моделирование
Для исследования вопросов сооружения гидроэлектростанций применяют метод гидравлических подобий, суть которого состоит в том, что в лабораторных условиях моделируются точно такие же условия, что и в натуре. Это явление называют физическим моделированием.
Например, чтобы два потока были подобными, требуется их:
1) геометрическое подобие, когда

где индексы н, м соответственно означают «натура» и «модель».
Однако, отношение

что значит, относительная шероховатость в модели такая же, как и в натуре;
2) кинематическое подобие, когда траектории соответствующих частиц, соответствующие линии тока подобны. Кроме того, если соответствующие части прошли подобные расстояния l н, l м, то отношение соответствующих времен движения выглядит следующим образом

где M i– масштаб времени
Такое же сходство имеется для скорости (масштаб скорости)

и ускорения (масштаб ускорения)

3) динамическое подобие, когда требуется, чтобы соответствующие силы были подобными, например, масштаб сил

Таким образом, если потоки жидкости механически подобны, то они подобны гидравлически; коэффициенты M l, M t, M υ, M pи прочие называются масштабными множителями.
45. Критерии гидродинамического подобия
Условия гидродинамического подобия требуют равенства всех сил, но это практически не удается.
По этой причине, подобие устанавливают по какой-нибудь из этих сил, которая в данном случае преобладает. Кроме того, требуется выполнение условий однозначности, которые включают в себя пограничные условия потока, основные физические характеристики и начальные условия.
Рассмотрим частный случай.
Преобладает влияние сил тяжести, например, при течении через отверстия или водосливы
P = ρgW. (1)
Если перейти к взаимоотношению P ни P ми выразить его в масштабных множителях, то
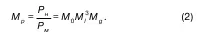
После необходимого преобразования, следует

Если теперь совершить переход от масштабных множителей к самим отношениям, то с учетом того, что l – характерный размер живого сечения, то
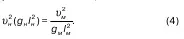
В (4) комплекс υ 2/gl называется критерием Фруди, который формулируется так: потоки, в которых преобладают силы тяжести, геометрически подобны, если

Это второе условие гидродинамического подобия.
Нами получены три критерия гидродинамического подобия
1. Критерий Ньютона (общие критерии).
2. Критерий Фруда.
3. Критерий Дарси.
Отметим только: в частных случаях гидродинамическое подобие может быть установлено также по
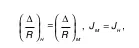
где Δ– абсолютная шероховатость;
R– гидравлический радиус;
J– гидравлический уклон
46. Распределение касательных напряжений при равномерном движении
При равномерном движении потеря напора на длине l heопределяется:
Читать дальшеИнтервал:
Закладка:






