Вадим Грибунин - Цифровая стеганография

Опишем распределения переменных стегосистемы, при которых достигается такая величина скрытой пропускной способности. Для данной стегосистемы переменную U можно формировать как U = X или U = Z , причем оба варианта выбора могут быть оптимальны, так как в качестве операции встраивания используется операция суммирования по модулю 2.

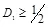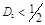Для и скрытая ПС равна 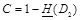. Заметим, что на первый взгляд удивительно, что при 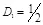скрытая ПС не равна нулю независимо от значения . Это объясняется тем, что при преобразовании скрываемого сообщения M в последовательность 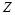искажение не является равновероятным: скрывающий информацию может выбрать такое распределение ошибок 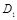, при котором минимизируется изменение сообщения M . Для 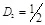скрытая ПС равна нулю при любых значениях 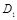. Нетрудно заметить, что при 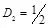выход 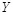канала связи не зависит от его входа X , что означает обрыв канала связи. И если при обрыве канала связи не передается никакой информации по открытому каналу связи, то тем более не передается по скрытому каналу, образованному на основе открытого канала.

Применим следствие 3.4 для анализа двоичной стегосистемы. Мы должны проверить, что распределения для 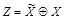и 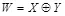имеют седловую точку платежа 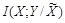. Сначала зафиксируем 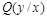. Полагая 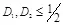, получим

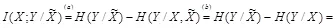
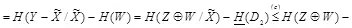
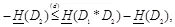
где равенство (а) справедливо в соответствии с определением условной взаимной информации, (b) выполняется благодаря тому, что 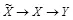есть марковская цепь, неравенство (с) справедливо, так как условие уменьшает энтропию. Равенство достигается в (с) если и только если 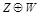, следовательно, 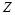независима от 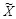. Неравенство (d) справедливо, так как Z и W независимы в силу того, что 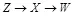формируют марковскую цепь и 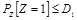. Равенство достигается, если переменная Z имеет бернуллиевское распределение с дисперсией 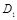. Распределение 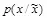удовлетворяет обоим неравенствам с равенством и поэтому максимизирует значение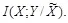

Второй шаг заключается в фиксации 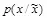и минимизации 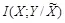над 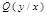. При определенном ранее распределени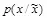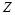и , и 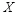независимы. Так как 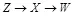формирует марковскую цепь, 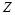и 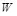также независимы.

Мы имеем

,

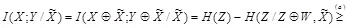
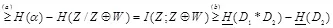где неравенство (а) справедливо, так как условие уменьшает энтропию, и неравенство (b) справедливо потому, что Z и W независимы и 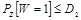, которое становится равенством, если W — переменная с бернуллиевским распределением с вероятностью единичного символа .

Рассмотренная двоичная стегосистема похожа на систему шифрования однократной подстановки (шифр гаммирования с бесконечной равновероятной независимой шифрующей гаммой). При независимой и равновероятной последовательности 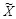выполняется равенство 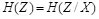, что означает, что эта система удовлетворяет требованию к совершенным криптосистемам [1], следовательно, перехват и анализ криптограммы Х не дает атакующему никакой информации о защищаемом сообщении Z . Однако эта двоичная система удовлетворяет также требованию к совершенным стеганографическим системам: распределения 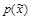и 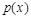идентичны, поэтому для нарушителя невозможно определить, принадлежат ли перехваченные данные к распределению 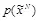пустых контейнеров или к распределению 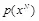стего со встроенным сообщением [17]. Подробно совершенные стегосистемы будут описаны в следующем разделе. Однако заметим, что в рассматриваемой стегосистеме предполагается, что контейнеры и, соответственно, стегограммы описываются бернуллиевским распределением, что обычно не характерно для реальных систем скрытия информации.

Рассмотрим пример двоичной стегосистемы с выбором U = Z . Пусть требуется скрытно передать сообщение M , которое является цифровым представлением речевого сигнала. Первые несколько отсчетов речевого сигнала в моменты времени дискретизации t 1 , t 2, t 3 , t 4принимают десятичные значения M 1= 0, M 2= 17, M 3= 35, M 4= 67 (рис. 3.4а). В общем виде скрываемое сообщение может быть представлено в виде M = ( M 1, M 2, M 3, M 4,). В двоичной форме скрываемое сообщение запишем как