Вадим Грибунин - Цифровая стеганография

M 1= 0000 0000, M 2= 0001 0001, M 3= 0010 0011, M 4= 0100 0011,

В данной записи младшие двоичные разряды расположены справа. Преобразуем двоичную последовательность M в двоичную последовательность Z с погрешностью 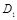. В двоичной стегосистеме погрешность кодирования 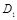вычисляется по метрике Хэмминга. Пусть искажение 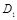= 1/8. Следовательно, для формирования последовательности 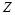= ( 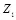, , 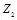, ,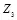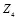…) скрывающий информацию искажает восьмую часть битов последовательности M . Для уменьшения погрешности скрываемого сообщения ему целесообразно искажать только младшие биты двоичной последовательности M . Поэтому скрывающий информацию выберет последовательность Z , например, такого вида: 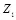= 0000 0001, 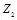= 0001 0010, 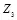= 0010 0011, 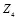= 0100 0010,…

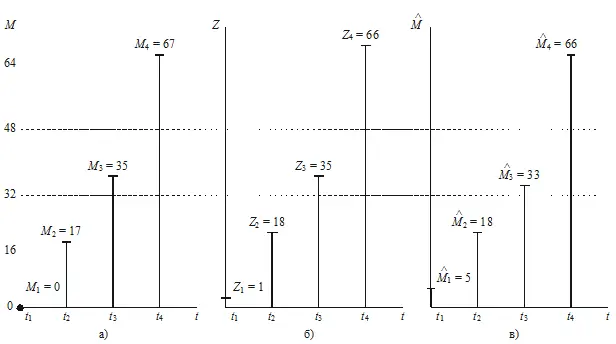
Рис. 3.4. Пример двоичной стегосистемы с искажениями D 1= 1/8 и D 2= 1/16

В десятичном виде последовательность Z показана на рис. 3.4б. C помощью генератора случайных чисел сформируем секретный ключ K = ( K 1, K 2, K 3, K 4, …).

K 1= 1001 0101, K 2= 0010 1110, K 3= 1101 1001, K 4= 0110 1001, …

Сформируем стегограмму по правилу 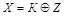, где X = ( , , , ,).

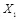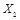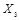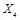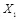= 1001 0100, 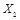= 0011 1100, 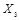= 1111 1010, 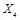= 0010 1011,

Пусть искажение = 1/16. Нарушитель случайным образом формирует двоичную последовательность W , в которой вероятность появления единичных символов равна . Например, W = ( 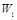, , 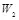, ,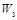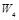) имеет вид

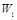= 0000 0100, 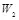= 0000 0000, 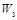= 0000 0010, 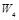= 0000 0000,

Атакующее воздействие представляет собой сложение по модулю 2 стегограммы X и шумовой последовательности W . Образованное искаженное стего Y = ( 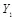, , 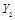, ,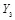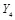) имеет вид

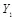= 1001 0000, 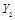= 0011 1100, 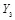= 1111 1000, 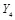= 0010 1011,

Получатель складывает последовательность Y с последовательностью ключа K для формирования принятой .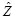

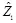= 0000 0101, 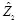= 0001 0010, 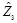= 0010 0001, 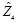= 0100 0010,

В декодере получатель восстанавливает сообщение M из последовательности 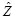. В самом простом случае 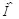= 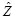. Вид последовательности 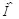показан на рис. 3.4 в. Если скрываемое сообщение представляет собой речевой сигнал, то при указанных величинах искажени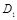й и степень близости M и 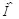, то есть качество обеспечиваемой скрытой телефонной связи, для ряда телекоммуникационных задач может быть оценено удовлетворительной.

Скрывающий информацию выбирает алфавит 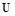и скрывающее преобразование 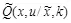из множества 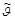. Атакующий выбирает атакующее воздействие 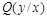из множества 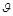. В теореме 3.3 предполагается, что атакующий знает распределение 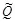, а декодер знает распределения Q и 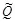. Это вполне разумное предположение, хотя оно может в некоторых случаях и не выполняться на практике. Рассмотрим теоретико-игровую постановку противоборства между скрывающим информацию и атакующим.

Скрывающий информацию. Он желает обеспечить гарантированную скорость безошибочной передачи при любой атаке, при которой атакующее воздействие приводит к величине искажения не более согласно выражения (3.7). Пусть он синтезирует стегосистему при предположении, что атакующий знает описание используемого скрывающего преобразования. При этом предположении скрывающий информацию может гарантировать, что минимальная скорость безошибочной передачи скрытой информации определяется выражением (3.9), которое для удобства повторяем:

.

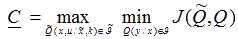Такой метод часто рассматривается как безопасная стратегия в теории игр [21]. Для максимизации скорости согласно выражения (3.9), декодер получателя должен знать описание используемого атакующего воздействия.