Вадим Грибунин - Цифровая стеганография
- Название:Цифровая стеганография
- Автор:
- Жанр:
- Издательство:Солон-Пресс
- Год:2002
- Город:Москва
- ISBN:5-98003-011-5
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Вадим Грибунин - Цифровая стеганография краткое содержание
Интерес к стеганографии появился в последнее десятилетие и вызван широким распространением мультимедийных технологий. Методы стеганографии позволяют не только скрытно передавать данные, но и решать задачи помехоустойчивой аутентификации, защиты информации от несанкционированного копирования, отслеживания распространения информации по сетям связи, поиска информации в мультимедийных базах данных.
Международные симпозиумы по скрытию данных проводятся с 1996 года, по стеганографии первый симпозиум состоялся в июле 2002 года. Стеганография – быстро и динамично развивающаяся наука, использующая методы и достижения криптографии, цифровой обработки сигналов, теории связи и информации.
На русском языке стеганографии было посвящено только несколько обзорных журнальных статей. Данная книга призвана восполнить существующий пробел. В ней обобщены самые последние результаты исследований зарубежных ученых. В книге рассмотрены как теоретические, так и практические аспекты стеганографии, выполнена классификация стегосистем и методов встраивания, детально исследованы вопросы повышения пропускной способности стегоканала, обеспечения стойкости и незаметности внедрения, приведено более 50 алгоритмов встраивания данных.
Книга предназначена для студентов, аспирантов, научных работников, изучающих вопросы защиты информации, а также для инженеров-проектировщиков средств защиты информации. Также несомненный интерес она вызовет у специалистов в области теории информации и цифровой обработки сигналов.
Цифровая стеганография - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
3. Выбор переменной U независимо от контейнера 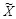 , как это делается в системе водяного знака согласно рис. 3.2, является в общем случае не оптимальным. Анализ выражения (3.8) показывает, что скорости безошибочной передачи в этом случае ограничены сверху величиной
, как это делается в системе водяного знака согласно рис. 3.2, является в общем случае не оптимальным. Анализ выражения (3.8) показывает, что скорости безошибочной передачи в этом случае ограничены сверху величиной 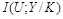 .
.
4. Пусть выполняется условие  ≥
≥ 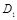 . Если атакующему известно описание контейнера
. Если атакующему известно описание контейнера 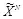 , то оптимальная атака состоит просто в формировании искаженного стего в виде
, то оптимальная атака состоит просто в формировании искаженного стего в виде 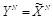 . В этом случае выходной сигнал после атакующего не содержит никаких следов сообщения и скрытая ПС равна нулю. На практике это означает следующее. Если нарушителю известен оригинал защищаемой от пиратского копирования мультимедийной информации, то никакие стегосистемы не защитят авторские и имущественные права производителей мультимедийной продукции.
. В этом случае выходной сигнал после атакующего не содержит никаких следов сообщения и скрытая ПС равна нулю. На практике это означает следующее. Если нарушителю известен оригинал защищаемой от пиратского копирования мультимедийной информации, то никакие стегосистемы не защитят авторские и имущественные права производителей мультимедийной продукции.
Рассмотрим потенциально сильную атаку, в которой атакующий стремится сконструировать достаточно близкую к оригиналу оценку контейнера 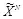 . Если атакующий способен синтезировать искаженное стего Y такое, что
. Если атакующий способен синтезировать искаженное стего Y такое, что 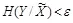 , то платеж ограничен сверху величиной
, то платеж ограничен сверху величиной
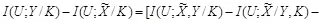
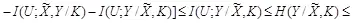
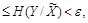 (3.12)
(3.12)
для всех U . Следовательно, величина скрытой ПС стегоканала 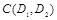 <
< 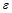 .
.
Таким образом, если нарушитель способен сформировать достаточно точную оценку контейнера (иными словами, выполняется неравенство 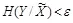 , где величина ε достаточно мала), то величина скрытой ПС ограничена этой малой величиной. А на практике это означает, что располагая подписанным водяным знаком стего, нарушитель может попытаться воспроизвести из него с некоторой допустимой погрешностью пустой контейнер, из которого удалено скрываемое сообщение. Такие примеры известны еще с доэлектронных времен стеганографии. Например, если перерисовать картину, заверенную художником малозаметными для визуального восприятия авторскими знаками, то хорошая копия может быть практически неотличима от оригинала (по крайней мере, для обычных зрителей), а авторские знаки, скорее всего, будут разрушены.
, где величина ε достаточно мала), то величина скрытой ПС ограничена этой малой величиной. А на практике это означает, что располагая подписанным водяным знаком стего, нарушитель может попытаться воспроизвести из него с некоторой допустимой погрешностью пустой контейнер, из которого удалено скрываемое сообщение. Такие примеры известны еще с доэлектронных времен стеганографии. Например, если перерисовать картину, заверенную художником малозаметными для визуального восприятия авторскими знаками, то хорошая копия может быть практически неотличима от оригинала (по крайней мере, для обычных зрителей), а авторские знаки, скорее всего, будут разрушены.
3.4. Двоичная стегосистема передачи скрываемых сообщений
Определим величину скрытой ПС стегосистемы, в которой алфавит скрываемых сообщений, контейнеров, ключей и стего является двоичным алфавитом 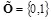 . Пусть контейнер
. Пусть контейнер 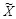 формируется источником Бернулли, то есть символы последовательности контейнера являются независимыми друг от друга и равновероятными. Функция искажения описывается расстоянием Хэмминга:
формируется источником Бернулли, то есть символы последовательности контейнера являются независимыми друг от друга и равновероятными. Функция искажения описывается расстоянием Хэмминга: 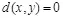 , если
, если 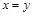 и
и 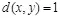 в ином случае. Описание контейнера является секретным ключом стегосистемы (
в ином случае. Описание контейнера является секретным ключом стегосистемы ( 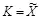 ) и известно декодеру. Пусть двоичная последовательность
) и известно декодеру. Пусть двоичная последовательность 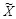 формируется независимо и равновероятно. Стегограммы формируются в виде
формируется независимо и равновероятно. Стегограммы формируются в виде 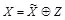 , где операция
, где операция 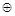 есть суммирование по модулю 2. Переменная Z имеет бернуллиевское распределение и отображает скрываемое сообщение M с искажением
есть суммирование по модулю 2. Переменная Z имеет бернуллиевское распределение и отображает скрываемое сообщение M с искажением 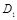 . Искажение
. Искажение 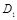 означает, что каждый символ двоичной последовательности Z отличается от соответствующего символа двоичной последовательности M с вероятностью
означает, что каждый символ двоичной последовательности Z отличается от соответствующего символа двоичной последовательности M с вероятностью 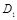 . Преобразование сообщения M в последовательность Z выполняется скрывающим информацию с использованием кодера с искажением
. Преобразование сообщения M в последовательность Z выполняется скрывающим информацию с использованием кодера с искажением 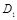 . Нарушитель обрабатывает стего наложением на него двоичной шумовой последовательности
. Нарушитель обрабатывает стего наложением на него двоичной шумовой последовательности 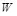 , в которой единичный символ порождается с вероятностью
, в которой единичный символ порождается с вероятностью  . Получатель суммирует искаженное стего
. Получатель суммирует искаженное стего 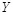 с двоичной последовательностью
с двоичной последовательностью 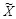 по модулю 2, и из полученной таким образом двоичной последовательности
по модулю 2, и из полученной таким образом двоичной последовательности 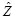 декодирует принятое скрываемое сообщение
декодирует принятое скрываемое сообщение 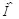 . Особенностью этой стегосистемы является то, что в ней скрываемое сообщение при встраивании искажается с вероятностью искажения
. Особенностью этой стегосистемы является то, что в ней скрываемое сообщение при встраивании искажается с вероятностью искажения 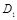 и это искажение равно искажению кодирования стего. Такая стегосистема показана на рис. 3.3.
и это искажение равно искажению кодирования стего. Такая стегосистема показана на рис. 3.3.
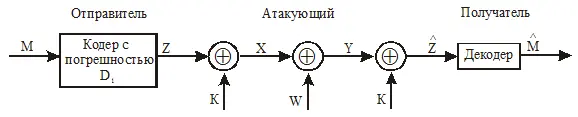
Рис. 3.3. Структурная схема двоичной стегосистемы
Утверждение 3.5: Для двоичной стегосистемы при величинах искажений 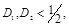 скрытая ПС определяется в виде
скрытая ПС определяется в виде
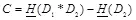 , (3.13)
, (3.13)
где, по определению, 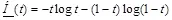 , и
, и 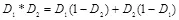 .
.
Оптимальная атака нарушителя определяется в виде 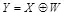 , где
, где 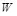 есть случайная двоичная последовательность, распределенная по бернуллиевскому закону с вероятностью появления единичного символа
есть случайная двоичная последовательность, распределенная по бернуллиевскому закону с вероятностью появления единичного символа  . Для
. Для 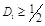 и
и 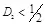 скрытая ПС равна
скрытая ПС равна 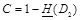 . Для
. Для 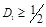 и
и 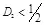 , скрытая ПС равна
, скрытая ПС равна 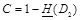 .
.
Интервал:
Закладка:










