Вадим Грибунин - Цифровая стеганография

Отметим, что в соответствии с выражением (3.19) для обеспечения ненулевой скрытой ПС при выполнении неравенства 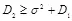вклад обоих слагаемых суммы 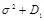равноценен. Это потенциально обеспечивает возможность маневра при синтезе стегосистем: увеличивать или искажение кодирования 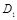при встраивании скрываемого сообщения или энергию контейнера, или сочетать оба подхода.

Для случая гауссовских контейнеров с распределением оптимальное атакующее воздействие легко синтезируется нарушителем. Атакующий просто заменяет стего шумовым сигналом, имеющим нормальное распределение с математическим ожиданием 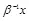и дисперсие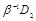й при 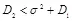. Если допустимое для нарушителя искажение достаточно велико, чтобы выполнилось неравенство 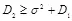, то согласно выражения (3.20) оптимальной стратегией нарушителя является, перехватив стего 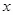, замена его на сигнал 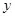, независимый от 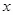. Такая атака достаточно просто реализуется на практике. Таким образом, чтобы гарантированно подавить канал скрытой связи, нарушителю надо внести в стего искажение величиной порядка энергии контейнера.

В целом недопустимо малая величина скорости передачи скрываемой информации при активном противодействии нарушителя является основным недостатком многих ранее предложенных системах водяного знака, в которых водяной знак прячется в наименее значимых битах контейнера, что является уязвимым даже к небольшим по величине искажениям . Такие водяные знаки легко удаляются атакующим простой рандомизацией наименее значимых битов, при этом в контейнер вносятся минимальные искажения. Следовательно, в более совершенных системах водяные знаки должны скрытно внедряться в существенно значащие компоненты контейнера. Однако при этом увеличивается величина искажения кодирования и поэтому ухудшается качество контейнера (что актуально для систем ЦВЗ) или ухудшается незаметность стегоканала (что актуально для систем скрытия от нарушителя факта передачи информации).

Таким образом, задача синтеза стегосистемы может быть сформулирована как задача поиска компромисса между ее характеристиками, так как улучшение одного ее параметра, например, величины скрытой ПС, приходится обеспечивать за счет других параметров, таких как скрытность передачи информации или устойчивость к разрушающему воздействию.

Рассмотрим стегосистему с бесконечным алфавитом, в которой декодеру получателя неизвестно описание использованного отправителем контейнера. Очевидно, что скорость достоверной передачи скрываемой информации в слепых системах не может быть выше, чем скорость передачи в случае, когда декодер имеет доступ к дополнительной информации, такой как использованный контейнер. Поэтому в слепых стеганографических системах величина скрытой ПС ограничена сверху выражением (3.19) для произвольных распределений 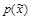контейнерных сигналов.

Рассматриваемая далее теорема 3.7 для слепых стегосистем определяет оптимальную стратегию скрывающего информацию и оптимальное атакующее воздействие для гауссовских контейнеров. Эта пара оптимальных стратегий противоборствующих сторон формирует решение седловой точки. Оптимальная атака нарушителя описывается гауссовским атакующим воздействием с распределением 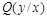согласно выражения (3.20). Теорема 3.7 также определяет величину скрытой ПС для слепых информационно-скрывающих систем.

Теорема 3.7.Пусть в слепой стегосистеме с бесконечным алфавитом 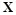используется среднеквадратическая мера искажения вида 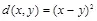. Контейнер 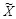описывается нормальным распределением с нулевым математическим ожиданием и дисперсией 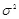. Тогда следующее построение стегосистемы дает седловую точку платежа в выражении (3.8):

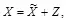
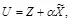
где коэффициенты принимают значения 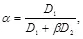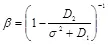, переменная 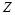описывается нормальным распределением с нулевым математическим ожиданием и дисперсией 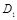и независима от контейнера 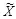, а распределение 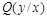описывает гауссовское атакующее воздействие вида (3.20). Величина скрытой ПС слепой стегосистемы определяется выражением (3.19).

Таким образом, в общем случае максимальная скорость безошибочной передачи скрытой информации не зависит от того, знает или нет декодер описание контейнера.

Прокомментируем суть теоремы 3.7.

1. Рассмотрим построение скрывающего преобразования в виде 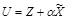, где значение 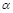отличается от оптимальной величины 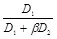. Скорость безошибочной передачи скрываемых сообщений определяется в виде:

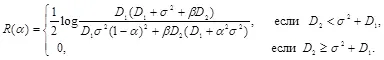(3.21)

Рассмотрим частный случай построения скрывающего преобразования, при котором коэффициент 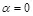. Это означает, что встраивание скрываемого сообщения совершенно не зависит от используемого контейнера 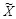. В явном виде этот вариант построения стегосистемы показан на рис. 3.2.