Вадим Грибунин - Цифровая стеганография

Из выражения (3.21) определим скорость безошибочной передачи для такого класса кодеров стегосистемы для случая малых искажений контейнера 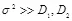в виде

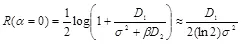. (3.22)

Игнорирование характеристик контейнера существенно уменьшает скорость надежной передачи скрываемой информации. Уменьшение величины скрытой ПС при отклонении от оптимального построения скрывающего преобразования наглядно показано на рис. 3.7. Из графика видно, насколько величина скрытой ПС при оптимальном построении (сплошная линия) превышает величину скрытой ПС при неиспользовании характеристик контейнера выбором 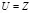(штрих-пунктирная линия). При заданных величине искажения = 1 и дисперсии контейнера 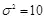игнорирование характеристик контейнера приводит к снижению величины скрытой ПС в десятки раз.

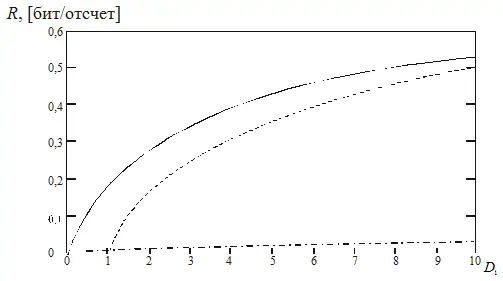
Рис. 3.7. Зависимость скрытой ПС стегоканала с гауссовским контейнером при 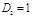и ,

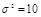оптимальное скрывающее преобразование,

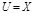скрывающее преобразование при ,

скрывающее преобразование при .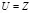

Для оптимального построения скрывающего преобразования, если искажение кодирования 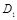существенно больше энергии контейнера 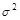, величина скрытой ПС очень мала. По мере увеличения величины искажения кодирования скрытая ПС быстро увеличивается, достигая максимума при .

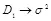2. Рассмотрим построение стегосистемы при выборе 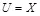(соответственно, 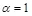). Практическая схема такой стегосистемы, в которой кодер построен по принципу кодовой книги, описана в [23]. Из выражения (3.21) следует, что максимальная скорость такой системы равна 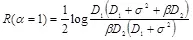. Можно показать, что скорость передачи скрываемых сообщений равна нулю для 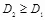. Следовательно, при выполнении неравенства 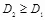такие стегосистемы нереализуемы. Зависимость скрытой ПС для случая вида 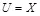показана на рис. 3.7 пунктирной линией при параметрах 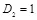и 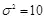. Из представленных графиков видно, что из-за неоптимальности построения стегосистемы для случая вида 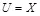максимальный проигрыш в величине скрытой ПС составляет порядка 0,15 бит на отсчет гауссовского контейнера.

Из двух рассмотренных случаев очевидно, что стегосистему целесообразно строить для выбора 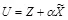, где .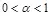

3. Рассмотрим возможные атаки нарушителя на слепую стегосистему с бесконечным алфавитом. Атака с аддитивным белым гауссовским шумом со средним значением 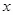и мощностью является в общем случае подоптимальной, но она становится асимптотически оптимальной при 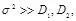так как в этом случае 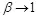. Напротив, атака, в которой делается попытка разрушить скрытое сообщение путем восстановления пустого контейнера 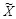из перехваченного стего с использованием правила максимальной апостериорной вероятности (МАВ) вида 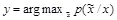, является совершенно неэффективной. В такой атаке 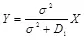, поэтому значения X и Y совпадают при 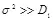. В этом случае условие 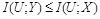выполняется с равенством и данная атака не способна удалить скрываемую информацию. Однако на практике такая стратегия действий нарушителя может быть достаточно эффективной, если законным получателем используется неоптимальный декодер, например, восстанавливающий водяные знаки при простом масштабировании яркости пикселов изображений, что приводит к невозможности обнаружения водяных знаков в таких декодерах.

4. На рис. 3.7 представлены зависимости достижимой скорости 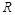безошибочной передачи для гауссовских контейнеров при различных информационно-скрывающих стратегиях. Скорость 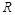является функцией от величины искажения 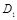при искажении 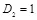с дисперсией контейнера 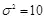. Показано, что при использовании оптимальной стратегии в каждом отсчете гауссовского контейнерного сигнала можно надежно передавать до 0,5 бит скрываемой информации (сплошная линия). В ряде работ приведены оценки достигнутых в реально построенных стегосистемах скоростей передачи скрываемой информации [4,5]. Достигнутые скорости во много раз меньше величины скрытой ПС, что должно стимулировать поиск более совершенных принципов построения стегосистем.

5. Вернемся к случаю малых искажений при 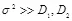. Из теории связи известно, что для достижения скорости 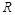безошибочной открытой передачи информации очень близкой к величине пропускной способности канала связи, требуется построить блочный код достаточно большой длины N , для которого количество кодовых комбинаций равно [25]. Соответственно, сложность реализации декодера системы открытой передачи пропорциональна числу вычислительных операций . В работе [2] показано, что для достижения скрытой ПС необходим блочный код с числом кодовых комбинаций не , а 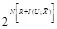. Соответственно, сложность реализации стегосистемы пропорциональна числу операций 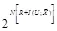. Величина 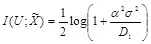обычно является существенно больше по сравнению со скоростью 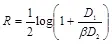. Следовательно, построить стегосистему со скоростью передачи скрываемой информации, приближающейся к величине скрытой ПС, значительно сложнее, чем построить систему передачи открытой информации со скоростью, приближающейся к величине ПС открытого канала связи.