Адам Кучарски - Идеальная ставка

Когда трейдеры реагируют на заметное событие – будь то публикация в Твиттере или большой заказ на продажу, – это привлекает внимание высокоскоростных алгоритмов, отслеживающих активность рынка. Если все продают акции, боты делают то же. При резком падении цен программы так же начинают подражать друг другу и тянут цены еще дальше вниз. Рынок превращается в стремительный конкурс красоты, где никто не хочет выбрать неправильную девушку. И скорость игры может создать немалые проблемы. Как понять, кто начал первым, если алгоритмы действуют молниеносно? «У вас нет времени на размышления, – говорит Фармер, – и это создает опасность чрезмерной реакции и стадного эффекта».

Трейдеры сообщают, что небольшие резкие обвалы на рынке случаются часто. Они не настолько серьезны, чтобы мелькать в заголовках газет, но все же достаточно заметны: то курс акций упадет буквально за долю секунды, то трейдинговая активность вдруг увеличится в сотни раз. И таких событий может быть несколько за один день. Когда ученые из Университета Майами изучали данные рынка акций в период с 2006 по 2011 год, то обнаружили сотни «чрезвычайно быстрых экстремальных событий», когда рынок стремительно падал или поднимался и затем возвращался в нормальное состояние менее чем за секунду. Нейл Джонсон, руководитель исследования, уверен, что ни в одной из традиционных финансовых теорий такие события не описаны даже приблизительно: «Люди не могут принимать участие в торгах в реальном времени, и теперь ситуацию контролируют супербыстрые роботы».

Говоря о теории хаоса, люди чаще всего думают о ее физическом аспекте. Они могут знать о работах Эдварда Лоренца и его «эффекте бабочки», описывавшем непредсказуемость погоды и возникновение торнадо в результате взмаха крыльев насекомого. Кто-то вспоминает эвдемонистов, рулетку и траекторию бильярдного шара, чувствительную к начальным условиям. Однако теория хаоса не ограничивается математикой и физикой. И пока эвдемонисты готовились к реализации своей рулеточной стратегии в Лас-Вегасе, на другом конце Соединенных Штатов эколог Роберт Мей разрабатывал теорию, которой суждено было в корне изменить наше представление о биологических системах.

Принстонский университет ничем не напоминает сверкающие небоскребы Лас-Вегаса. Кампус – настоящий лабиринт из неоготических зданий и тенистых дворов. В зарослях плюща носятся белки, на нью-джерсийском ветру развеваются форменные черно-оранжевые шарфы студентов. Если присмотреться, здесь повсюду отыщутся следы пребывания знаменитых обитателей Принстона. Эйнштейн-драйв огибает Институт перспективных исследований, невдалеке находится «перекресток фон Неймана», названный в честь автомобильных аварий, в которые не раз попадал ученый. История гласит, что один из дорожных инцидентов фон Нейман объяснил особенно оригинально: «Я ехал по дороге, а деревья организованно двигались по правую сторону со скоростью шестьдесят миль в час. Внезапно одно из них стало на моем пути».

В 1970-х Мей преподавал в университете зоологию и большую часть времени проводил за изучением сообществ животных. Особенно его интересовали колебания численности популяций. Чтобы понять, как различные факторы влияют на экологические системы, Мей построил несколько простых математических моделей роста популяций.

С математической точки зрения самый простой тип популяции – тот, в котором размножение происходит путем дискретного всплеска. К примеру, многие виды насекомых в средних широтах дают потомство раз в сезон. Экологи могут изучать поведение гипотетической популяции насекомых, используя уравнение под названием «логистическая карта». Впервые его предложил в 1838 году статистик Пьер Верхюльст, исследовавший потенциальные границы роста популяции. Для расчета плотности популяции в заданном году с помощью логистической карты необходимо перемножить три показателя: показатель прироста популяции, плотность популяции в предыдущий год и величину доступного пространства и, следовательно, ресурсов.

Математически это выглядит так:

Логистическая карта построена на простом наборе предположений, и при небольшом приросте популяции результат тоже получается простым. Через несколько сезонов популяция приходит в равновесие, и в последующие годы ее плотность остается одинаковой.

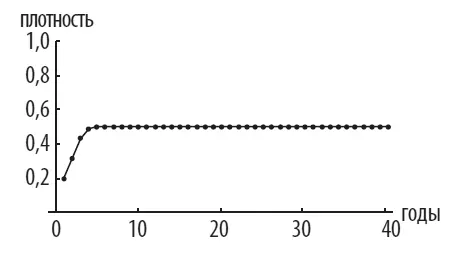
Показатели логистической карты при низком приросте популяции

Ситуация меняется с увеличением прироста, которое влечет за собой колебания плотности популяции. В каком-то году на свет появляется множество насекомых, что снижает количество доступных ресурсов, в следующем году выживает меньшее количество особей, освобождается пространство и ресурсы для следующего поколения и так далее. На рисунке ниже схематически изображено изменение популяции.

Но если прирост очень велик, начинает происходить нечто странное. Вместо того чтобы прийти к фиксированным показателям или меняться в предсказуемых пределах, плотность популяции начинает сильно колебаться.

Напомним, в этой модели нет хаотичности, нет случайных событий. Плотность популяции животных зависит от простого линейного уравнения.

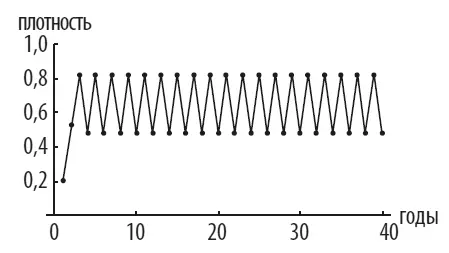
Колебание плотности популяции со средним приростом

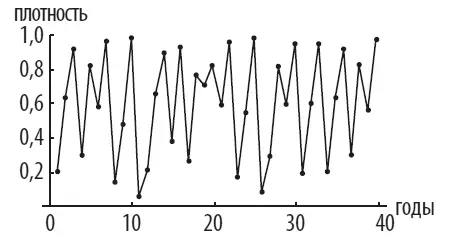
Неустойчивая динамика популяции как следствие высокого прироста

В результате мы получаем полную мешанину показателей, явно не вписывающихся ни в какой осмысленный паттерн.

Мей попытался объяснить происходящее с помощью теории хаоса. Перепады плотности популяции были результатом реакции на начальные условия. Здесь, как и в случае с траекторией шарика рулетки, которую изучал Пуанкаре, небольшие изменения в начальной обстановке оказывали огромное влияние на дальнейшее развитие ситуации. Несмотря на то что популяция подчиняется простым биологическим законам, предугадать, как будут развиваться события в отдаленном будущем, невозможно.

От рулетки мы привыкли ждать неожиданностей, но экологи были крайне удивлены, обнаружив, что такая простая формула, как логистическая карта, способна запустить столь сложные процессы. Мей предупреждал, что наблюдать столь же причудливые результаты можно и в других сферах жизни. Необходимо помнить, что и в политике, и в экономике простые схемы не всегда ведут себя просто.