Чарльз Петцольд - Код. Тайный язык информатики

Цикл осциллятора — интервал, в течение которого его выход изменяется, после чего возвращается к исходному значению.

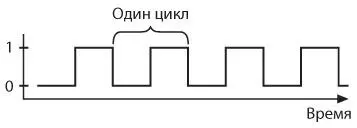
Время, которое занимает один цикл, называется периодом осциллятора. Предположим, период нашего осциллятора равен 0,05 секунды. Вдоль горизонтальной оси мы можем отложить время в секундах начиная с некоторого произвольно выбранного нулевого момента.

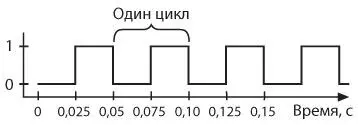
Частота осциллятора равна единице, поделенной на период. В данном примере, если период осциллятора составляет 0,05 секунды, его частота 1 / 0,05 = 20 колебаний в секунду . Выход осциллятора изменяется и возвращается к исходному значению 20 раз в секунду.

Количество колебаний в секунду — такой же логичный термин, как количество километров в час , килограммов на квадратный метр или калорий на порцию , однако он больше не используется. В память о Генрихе Рудольфе Герце (1857–1894), который первым передал и принял радиоволны, говорят « герц» . Сначала это слово начали применять в Германии в 1920-х годах, а затем за несколько десятилетий термин прижился и в других странах.

Таким образом, можно сказать, что наш осциллятор имеет частоту 20 герц, или 20 Гц (сокращенно).

Конечно, мы произвольно указали частоту одного конкретного осциллятора. В конце этой главы мы сможем соорудить то, что позволит фактически измерить данный параметр.

Чтобы начать работу над этим устройством, давайте рассмотрим пару вентилей ИЛИ-НЕ, соединенных определенным образом. Вероятно, вы помните, что на выходе вентиля ИЛИ-НЕ есть напряжение, только если напряжения нет ни на одном из его входов.

Вот схема с двумя вентилями ИЛИ-НЕ, двумя переключателями и лампочкой.

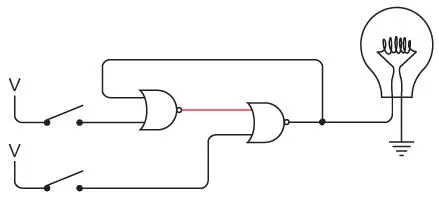
Обратите внимание на необычную схему проводки: выход левого вентиля ИЛИ-НЕ — это вход правого вентиля ИЛИ-НЕ, а выход правого вентиля ИЛИ-НЕ — вход левого вентиля ИЛИ-НЕ. Такое соединение называется обратной связью . Действительно, как и в случае с осциллятором, выход становится входом. Эта особенность будет характерна для большинства схем, приведенных в данной главе.

Сначала ток в этой цепи будет течь только от выхода левого вентиля ИЛИ-НЕ. Это связано с тем, что оба входа данного вентиля равны 0. Теперь замкните верхний переключатель. Выход левого вентиля ИЛИ-НЕ становится равным 0, а это значит, что выход правого вентиля ИЛИ-НЕ равен 1, и лампочка загорается.

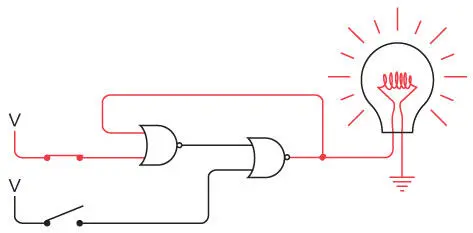
Волшебство наблюдается, когда вы размыкаете верхний переключатель. Поскольку выход вентиля ИЛИ-НЕ — 0, если один из входов — 1, выход левого вентиля ИЛИ-НЕ не изменяется, и лампочка не гаснет.

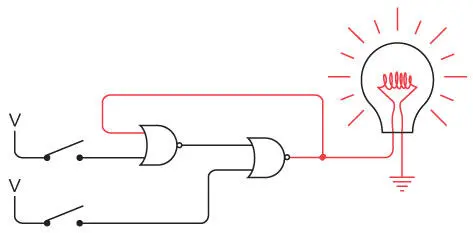
Не кажется ли вам это странным? Оба переключателя разомкнуты, как и на первом рисунке, однако теперь лампочка горит. Эта ситуация, безусловно, отличается от тех, что мы видели ранее. Обычно выход цепи зависит только от ее входов. Похоже, в данном случае это не так. Более того, на этом этапе вы можете замкнуть и разомкнуть верхний переключатель, и лампочка не погаснет. Этот переключатель больше не влияет на цепь, поскольку выход левого вентиля ИЛИ-НЕ остается равным 0.

Теперь замкните нижний переключатель. Поскольку один из входов правого вентиля ИЛИ-НЕ равен 1, выход становится равным 0, лампочка гаснет. При этом выход левого вентиля ИЛИ-НЕ — 1.

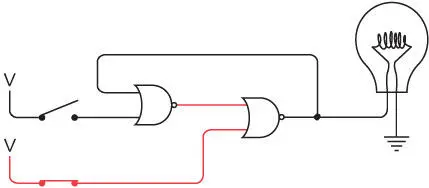
Если вы разомкнете нижний переключатель, лампочка останется выключенной.

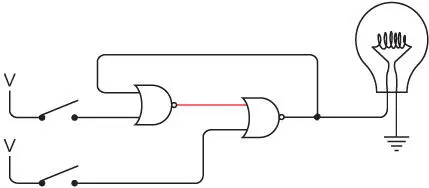
Мы вернулись туда, откуда начали. Теперь вы можете замкнуть и разомкнуть нижний переключатель, не повлияв на лампочку. Подытожим:

при замыкании верхнего переключателя лампочка загорается и остается гореть при размыкании верхнего переключателя;

при замыкании нижнего переключателя лампочка гаснет и не загорается при размыкании нижнего переключателя.

Странность этой схемы заключается в том, что, когда оба переключателя разомкнуты, иногда лампочка горит, иногда — нет. Можно сказать, что эта схема имеет два устойчивых состояния , когда оба переключателя разомкнуты. Называется такая схема триггером , и его история началась в 1918 году с работы английского радиофизика Уильяма Генри Эклза (1875–1966) и Фрэнка Джордана (о котором мало что известно).

Триггер сохраняет информацию , «помнит». В частности, показанный ранее триггер помнит, какой переключатель был замкнут последним. Если вы столкнулись с таким триггером и видите, что лампочка горит, можете предположить, что последним был замкнут верхний переключатель; если лампочка не горит — нижний.

Триггер похож на качели, которые имеют два устойчивых состояния, никогда подолгу не задерживаются в неустойчивом среднем положении. Глядя на качели, вы всегда можете сказать, в какую сторону они качнулись в последний раз.

Возможно, это не является очевидным, однако триггеры весьма полезны. Они обеспечивают память схемы, сохраняющую историю того, что произошло ранее. Представьте, что значит считать, не обладая памятью. В этом случае вы не знаете, какое число задумали, какое число следует к нему прибавить! Точно так же схема , которая производит подсчет (описанная далее), требует наличия триггеров.

Существуют два различных типа триггеров. Тот, что я показал выше, является самым простым и называется RS-триггером (Reset/Set, сброс/установка). Два вентиля ИЛИ-НЕ чаще всего изображаются и обозначаются так, как показано на диаграмме, для придания им симметричного вида.

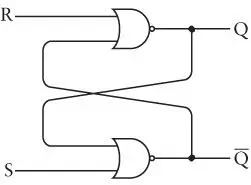
Выход, который мы использовали для лампочки, традиционно называется Q (от английского quit — «выход»). Кроме того, существует второй выход 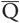, который является электрически противоположным выходу Q, то есть инверсией Q. Если Q равен 0, то Q равен 1, и наоборот. Два входа, S и R, используются для установки (set) и сброса (reset). Вы можете думать об этих действиях так: «установить значение Q на 1» и «сбросить значение Q на 0». Когда S равно 1 (что соответствует замыканию верхнего переключателя на приведенной раннее диаграмме), выход Q становится равным 1, а выход — 0. Когда R равен 1 (что соответствует замыканию нижнего переключателя на приведенной ранее диаграмме), выход Q становится равным 0, а выход — 1. Когда оба входа равны 0, выход указывает на то, являлось ли последним действием установка или сброс значения Q. Результаты работы этой схемы приведены в следующей таблице.