Чарльз Петцольд - Код. Тайный язык информатики

И так до бесконечности. Подобная дробь называется периодической и записывается 0,(3). Несмотря на то что запись числа ⅓ в виде десятичной дроби выглядит неуклюже, это число по-прежнему является рациональным, поскольку это отношение двух целых чисел. Вот еще один пример: отношение 1/7 можно записать в виде десятичной дроби.

0,1428571428571428571428571428571428571428571428571428571…

Или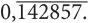

Иррациональные числа — это числа, которые нельзя выразить в виде отношения двух целых чисел, значит, десятичная дробь продолжается бесконечно без повторяющихся последовательностей цифр. К числам такого типа относится квадратный корень из 2.

√2 ≈ 1,41421356237309504880168872420969807856967187537695…

Квадратный корень из 2 — решение следующего алгебраического уравнения:

x2 – 2 = 0.

Если число не является решением какого-либо алгебраического уравнения с целочисленными коэффициентами, оно называется трансцендентным . (Все трансцендентные числа иррациональны, однако не все иррациональные числа трансцендентны.) К трансцендентным числам относится число π, представляющее отношение длины окружности к ее диаметру и приблизительно равное следующему.

3,1415926535897932846264338327950288419716939937511…

Еще одним трансцендентным числом является e , к которому стремится выражение:

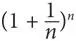
при n , стремящемся к бесконечности. Данное число приблизительно равно следующему.

2,71828182845904523536028747135266249775724709369996…

Все числа, о которых мы говорили, то есть рациональные и иррациональные, называются действительными, или вещественными . Это обозначение отличает их от мнимых — квадратных корней из отрицательных чисел. Комплексные числа — это комбинации мнимых и вещественных чисел. Несмотря на свое название, мнимые числа существуют и используются, например при решении некоторых сложных задач по электронике.

Мы привыкли считать, что числовой ряд непрерывен . Если вы дадите два рациональных числа, я определю, какое число находится между ними. Для этого достаточно найти их среднее арифметическое. Однако цифровые компьютеры не могут работать с континуумами. Биты могут быть равны либо 0, либо 1, между которыми нет больше никаких значений. Так что цифровые компьютеры могут иметь дело только с дискретными значениями. Количество дискретных значений, которые вы можете представить, напрямую связано с количеством доступных битов. Например, в ячейках емкостью 32 бита можно хранить положительные целые числа в диапазоне от 0 до 4 294 967 295. При необходимости сохранить значение 4,5 придется пересмотреть этот подход и действовать иначе.

Можно ли представить дробные значения в двоичном формате? Да, можно. Вероятно, самый простой подход — использование двоично-десятичного кода (BCD). Как говорилось в главе 19, кодировка BCD позволяет записать десятичные числа в двоичном формате. Для кодирования каждой десятичной цифры (0, 1, 2, 3, 4, 5, 6, 7, 8 и 9) требуется четыре бита.

Десятичная цифра

Двоичное значение

0

0000

1

0001

2

0010

3

0011

4

0100

5

0101

6

0110

7

0111

8

1000

9

1001

Формат BCD особенно полезен в компьютерных программах, которые работают с денежными суммами. Самые очевидные примеры — программы для банков и страховых компаний; многие дробные числа в них предусматривают не более двух знаков после десятичного разделителя.

Как правило, для хранения двух BCD-цифр достаточно одного байта. Такая система записи иногда называется упакованным кодом ВСD . В такой кодировке не используется дополнение до двух. По этой причине в случае упакованного кода BCD для указания того, является ли число положительным или отрицательным, обычно требуется дополнительный бит, называемый знаковым битом . Поскольку для хранения BCD-значения удобно выделять целое число байтов, под бит знака обычно отводится четыре или восемь бит памяти.

Предположим, что сумма денег, которой должна оперировать ваша компьютерная программа, никогда не превысит ±10 миллионов долларов. Другими словами, вам требуются значения от –9 999 999,99 до 9 999 999,99. Можно выделить по пять байт памяти для каждой сохраняемой суммы в долларах. Например, число –4 325 120,25 можно представить посредством пяти байт.

В шестнадцатеричном формате это эквивалентно следующей записи.

Обратите внимание: крайняя левая тетрада равна 1, то есть число является отрицательным. Это знаковый бит. Если бы число было положительным, то крайняя левая тетрада была бы равна 0. Для представления каждой цифры в числе требуется по четыре бита, а прочитать их можно непосредственно по шестнадцатеричным значениям, поскольку они совпадают с десятичными.

Для представления значений в диапазоне от –9 999 999,99 до 9 999 999,99 вам понадобится шесть байт: пять байт для десяти цифр и еще целый байт для знакового бита.

Такой формат записи дробных чисел называется записью с фиксированной точкой , поскольку после десятичного разделителя всегда следует определенное количество цифр, в нашем примере две. Важно: данные о положении этого разделителя не хранятся вместе с числом. Программам, работающим с числами в таком формате, необходимо сообщить, где находится этот разделитель. Вы можете создавать числа с любым количеством десятичных знаков, а также использовать их в одной и той же компьютерной программе. Однако любая часть программы, выполняющая над числами арифметические операции, должна знать, где находится десятичный разделитель.

Формат с фиксированной точкой хорошо работает только в том случае, если вы уверены, что числа не превысят размеры выделенных под них ячеек памяти, что вам не потребуется увеличивать количество десятичных знаков. Использование этого формата совершенно неуместно в ситуациях, когда числа могут стать слишком большими или маленькими. Предположим, вам нужно зарезервировать область памяти для хранения расстояний. Проблема в том, что эти расстояния могут значительно варьироваться. Расстояние от Земли до Солнца составляет 150 000 000 000 метров, а радиус атома водорода — 0,00000000005 метра. Для хранения значений в формате с фиксированной точкой, принадлежащих этому диапазону, придется выделить 12 байт памяти.

Возможно, мы сможем придумать более удобный способ хранения таких чисел, если вспомним, что ученые и инженеры выражают числа с помощью системы, называемой научной нотацией ( экспоненциальная запись ).