Альманах «Знак вопроса» - Знак вопроса, 2005 № 01

Первый сын, вдова, несчастный брак,

Совсем без детей, два Острова в ссоре,

Нет восемнадцати, еще несовершеннолетним.

Другой будет помолвлен еще моложе.

Давайте, обратим внимание, что ему шел восемнадцатый год — это и будет первая цифра от суммы в номере катрена. Его возраст я хочу закрепить тем, что его жена Мария Стюарт — рождения 1542 года. Она была шотландской королевой и в тот период заявила о своих правах на английский престол. Франциск II умер 5 декабря 1560 года.

Вторым на престол взошел под символом Каппа Карл IX, сначала из-за малолетства (ему шел только 11 год) регентшей была его мать Екатерина Медичи. Обручен Карл IX был с принцессой Елизаветой Австрийской в 1561 году. За время своего правления он прославит себя как король устрашения с небес, которому Нострадамус посвятит катрен 72 в Центурии X. Это событие было отмечено Варфоломеевской ночью, устроенной братьями Гиз 24 августа 1572 года. За одну ночь в городах Франции было уничтожено 20 тысяч протестантов — кальвинистов-гугенотов. И он закончит свое правление в 1574 году, будучи отравлен. Итак, он проживет период от 1550 до 1574 и умрет на 25 году своей жизни.

Теперь, если мы прибавим время жизни Карла IX — 25 лет — ко времени жизни Франциска II — 18 лет, то мы получим сумму, равную 43 годам.

Третьим на престол Франции взойдет Генрих III Анжуйский, последний из братьев. Здесь фигурирует символ — буква греческая Ламбда, так как он будет фактически убит своими сподвижниками из Лиги братьев-католиков Гизов, за которых ему отомстят и убьют его на 38-м году жизни в 1589 году. Убийство было организовано при участии католической Испании.

Вот теперь мы видим полную разгадку номера катрена 81, если к периоду жизни Генриха III — 38 лет — мы прибавим сумму прожитых лет двух его братьев, Франциска II и Карла IX — 43 года, то мы получим долгожданную разгадку шифра катрена — общую сумму лет в 81 год, что и соответствует номеру катрена 81.

11 августа 2004 года.

Сегодня 24 сентября 2004 года.

И самое главное, и завершающие слова четвертой строки — и на век . — То есть этим самым завершается правление во Франции династии Валуа. С 1589 года к власти приходит династия Бурбонов в образе Генриха IV Наваррского. Вот весь стопроцентный расклад данного катрена 81.

Хочется выразить благодарность журналу «Знак вопроса» за публикацию статьи ВИРТУАЛЬНАЯ ИГРА «ОТОБРАЖЕНИЕ», которая появилась в № 1/2004 на с. 107 и в № 3/2004 на с. 125. Автору пришлось обращаться более чем в 30 °CМИ с предложением игры и ее публикации, но получал отказ. Причина одна: мы это не проходили ни в средней, ни в высшей школе?! Спрашивается — как же будет пробивать себе дорогу все новое в России, если требуется публиковать то, что уже известно. Я сообщаю этот факт к тому, чтобы читатель понял, что виртуальные игры «отображение» — В.И.О. носят факультативный характер и предназначены для молодежи и любознательных от природы людей. Кроме того В.И.О. формирует понятие о критериях ресурсосбережения и унификации. В свою очередь критерии ресурсосбережения и унификации позволяют достигать определенного уровня эффекта эмерджентности в структурах и системах при отображении визуальных образов в вербальные, и наоборот.

В прошлых публикациях рассматривалось отображение двух правильных треугольников в три правильных шестиугольника и двух одинаковых прямоугольников в три разномасштабных прямоугольника, при одном и том же числовом выражении формы — П. В настоящей статье мы рассмотрим отображение трех ромбов в четыре правильных шестиугольника и трех прямоугольников с соотношением сторон 1: 2 в четыре восьмиугольника, кроме того мы рассмотрим отображение трех равновеликих квадратов в четыре разномасштабных квадрата. Каждое отображение будет комментироваться с точки зрения критериев ресурсосбережения. Напомним, что отображение происходит при постоянном числовом выражении формы — П.

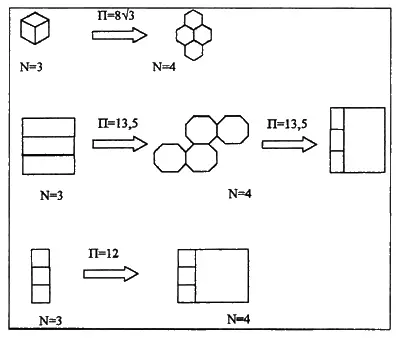
Ответ на игру, связанную с отображением египетских треугольников. Египетский треугольник с числовым выражением формы П = 7,5 может быть отображен двумя фигурами в форме пятиугольников, вписанных в шестиугольник. Изображение дается на рис. 1. Необходимо отметить, что когда мы отображаем фигуру или объем, то отображение обладает изопериметрическими свойствами. Поясним это примерами. Два пятиугольника вписанные в шестиугольник, имеют значение фактора П = 3,75 + 3,75 = 7,5. Это значение минимально. Если же одну из вертикальных сторон сначала уменьшим до величины 1,4, т. е. Р = 2,0 + 1.4 + 1,25 + 1,25 + 1,4 + 2,0 + 1,4 + 1,25 + 1,25 + 1,5 = 14,6; L = 7,3; F = 7,1; П = 7,505, а затем увеличим до 1,6 единицы, т. е. Р = 2,0 + 1,6 +1,25 + 1,25 +1,6 + 2,0 + 1,6 + 1,25 + 1,25 + 1,6 = 15,4; L = 7,7; F = 7,9; П = 7,505, то увидим, что при отклонении значения вертикальной стороны от величины 1,5 происходит увеличение фактора П = 7,505 на пять тысячных. Это эмерджентные или изопериметрические свойства планировочной структуры изображенной на рис. 1 с фактором П = 7.5 являются определенной целью В.И.О. В качестве примечания следует отметить, что изображенное на рис. 1 отображение можно рассматривать как обратное действие по триангуляции планировочной структуры состоящей из двух пятиугольников вписанных в шестиугольник на египетский треугольник с фактором П = 7,5. Такое же действие связано с триангуляцией двух «полукубов» на египетский треугольник с фактором П = 6,0 (рис. 1).

Об авторе:

Куштанин Кобальт Иванович — инженер-разработчик оптических приборов, автор 33 изобретений, книги по лазерной и волоконной оптике. Печатался в журнале «Инженер».

Ж. И. Алферов получил Нобелевскую премию по физике. После заслуженных похвал лауреату и гордости за свою страну возникает вопрос: почему опять награду получил физик? Нобелевских премий по науке пять: по физике, химии, медицине, физиологии и экономике. Наши ученые получили после 1917 г. шесть премий по физике и одну математик — по экономической науке. До 1917 г. Нобелевские премии получили И.П.

Павлов и И. М. Сеченов по медицине и физиологии. А до 1917 г. физика в стране была в загоне и по своему уровню отставала от математики, химии и биологии. Физика стала развиваться после того, как было снято удушавшее ее правило о магистерском экзамене по математике для физиков, и в страну после Октября вернулись несколько крупных ученых. Причина советского перекоса в физику лежит не в особенностях наших мозгов, а в истории страны и выходит за рамки чистой науки.