Олег Власов - Футболоматика: как благодаря математике «Барселона» выигрывает, Роналду забивает, а букмекеры зарабатывают состояния

И хотя модель размножения бактерий, разработанная Лией, может кого-то повеселить, она явно неправильная. Чтобы такая модель работала, наша планета должна быть одним огромным куском мяса. Но это не так. Оптимальное описание роста должно учитывать некие ограничения. Если бы у нас было 20 тысяч болельщиков «Вест Хэм Юнайтед», распевающих «I’m Forever Blowing Bubbles» («Я всегда надуваю пузыри») на «Аптон Парк», вмещающем 35 016 человек, другим 20 тысячам поющих фанатов просто не хватило бы места. После переезда «Вест Хэма» на Олимпийский стадион матчи команды могут посетить примерно 60 тысяч болельщиков, однако уйдет ненамного больше времени на то, чтобы пение охватило весь этот стадион. Если мы умножим 40 тысяч на два, мы получим 80 тысяч – а это значит, что лимит количества поющих фанатов достигнут.

Ответом на данную проблему моделирования является S-образная кривая – самая эффективная и универсальная математическая модель роста. Для того чтобы получить такую кривую, нам нужны всего два условия. Первое – такое же, как и для составления геометрической прогрессии: каждого поющего болельщика подхватывает другой болельщик, который до этого не пел. Затем отметим, что количество фанатов ограниченно: каждый болельщик может начать петь только один раз. Объединив эти два условия, мы получим S-образную кривую роста (см. рисунок 10.1) [113] Здесь я даю более подробный вывод кривой логистического роста. Согласно двум предположениям, общая скорость начала пения в следующем раунде пропорциональна 2 х ( n – x ), где n – количество поклонников, а x – это число фанатов, начавших петь. Этот показатель роста приведен ниже. Когда x мало, пение распространяется медленно, потому что певцов слишком мало. Кроме того, когда x близок к n , пение распространяется медленно, потому что для участия в нем доступно меньше людей. Из кривой видно, что максимальное увеличение происходит в точке n /2, когда половина фанатов уже поют, а вторая может присоединиться. . В самом начале рост будет медленным, однако он будет происходить в геометрической прогрессии.

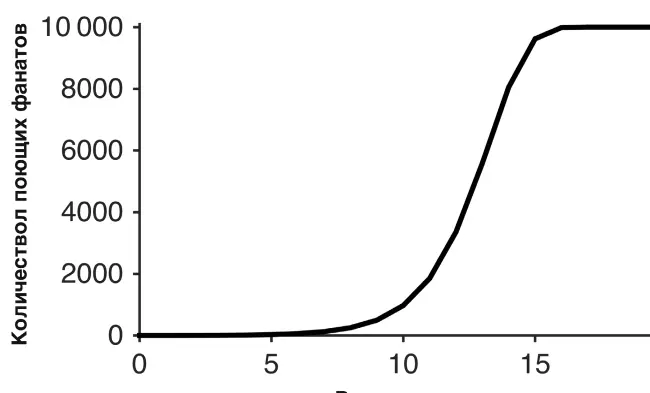
Рисунок 10.1. Постепенное увеличение количества поющих болельщиков через социальное заражение.

Количество поющих фанатов в каждом «раунде» увеличивается вдвое. Как только пением охватывается половина стадиона, рост снова замедляется и показатель в итоге стабилизируется на отметке, когда поют абсолютно все. Нужно всего 16 раундов, чтобы чант подхватили 10 тысяч фанатов.

Распространение идей, распространение болезни, распространение пения на стадионе – все это формы заражения. Когда мы распеваем чанты, заражение будет считаться социальным: пение распространяется людьми, которые слушают других и повторяют друг за другом. Некоторые инфекционные заболевания, такие как ВИЧ, Эбола, грипп и атипичная пневмония, передаются при тесном контакте людей. Другие заболевания, такие как холера и отдельные разновидности гепатита, передаются через зараженную воду или пищу. Независимо от способа распространения таких болезней рост количества заболевших можно представить в виде S-образной кривой. Вначале мы наблюдаем небольшое число случаев заболевания, но затем в игру вступает геометрическая прогрессия, и болезнь принимает огромные масштабы. И на данном этапе все, на что мы можем надеяться, – это предотвращение негативных последствий. Важно убедиться в том, что количество инфицированных людей стабилизируется, пока не будет поздно.

Не так уж легко подтвердить или опровергнуть аналогию между распространением заболевания и распеванием чантов. Непросто проводить контролируемый эксперимент в условиях футбольного матча. Я мог бы, конечно, стать на трибуне и завести «Seven Nation Army», а потом посмотреть, запоет ли кто-нибудь вместе со мной. Однако что-то мне подсказывает, что никто не обратит особого внимания на одинокого математика. Более подходящее место для проведения опытов с аплодисментами – это учебная аудитория, что, собственно, и выбрали для своих исследований мои коллеги Йенс Краузе и Джолион Фариа [114] Mann, R.P. The dynamics of audience applause. – Journal of the Royal Society Interface 10(85), 2013. – 20130466. . Они попросили несколько групп первокурсников поприсутствовать на семинаре, который проводил студент последнего курса. Заданием, которое Йенс и Джолион дали студентам младшего курса, было составить свое мнение о презентации и сделать пометки, а также обязательно выражать поддержку или одобрение выступающему аплодисментами. Студенты знали, что их снимают, но они и понятия не имели о том, что главной целью данного эксперимента было посмотреть, как именно они будут аплодировать. Если бы им заранее сказали о том, что мы наблюдаем за тем, как они хлопают, они бы, вероятнее всего, засмущались, а это отразилось бы на их поведении.

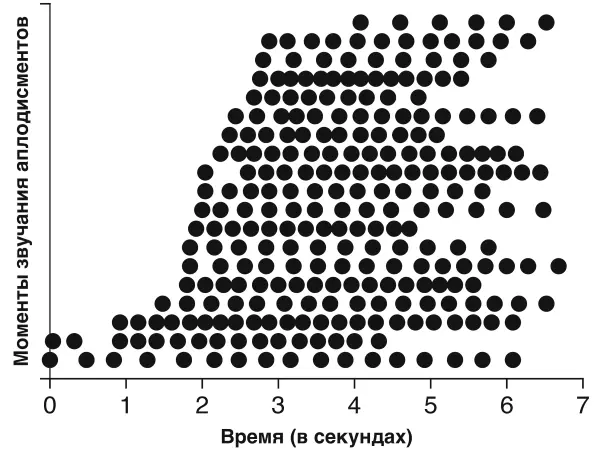
Рисунок 10.2. Моменты, когда звучали аплодисменты, в динамике. Каждая точка – это хлопки одного студента в ходе одного раунда аплодисментов. На основе рисунка, созданного Ричардом Манном.

Отметив каждый момент времени, когда студенты начинали аплодировать, мы можем наблюдать то, как распределились аплодисменты, звучавшие в аудитории. Хлопки одной группы студентов изображены на рисунке 10.2. Каждый ряд – это хлопки одного человека, а каждая точка – это один «раунд», когда совершались хлопки. Студенты представлены в определенном порядке, начиная с тех, кто первым стал аплодировать. Второй снизу ряд – это студент, который был первым, кто закончил аплодировать, и вторым, кто начал.

Аплодисменты студентов звучали неравномерно: кто-то начинал раньше, кто-то – позже. Некоторые студенты аплодировали энергично, некоторые – более сдержанно. Представив полученные данные в виде такого рисунка, мы четко видим то, как распределились аплодисменты в одной группе.

Такой способ представления результатов позволяет нам выявить факторы того, почему человек начинает аплодировать. Вместе с Ричардом Манном, исследователем из моей группы, мы изучили весь набор возможных причин того, почему люди начинают аплодировать. Происходило ли это сразу после того, как начинали аплодировать другие? Зависело ли это от того, аплодирует ли тот человек, который сидит рядом? Важно ли было то, насколько интенсивно хлопают остальные? Или же люди хлопали в ладоши абсолютно произвольно, вне зависимости от каких-либо факторов? Мы пришли к выводу, что оптимальная модель основывается на количественном соотношении людей, которые уже аплодируют: чем больше было тех, кто хлопает в ладоши, тем быстрее остальные присоединялись к ним. Аплодисменты – это социальное заражение.