Микаэль Лонэ - Большой роман о математике. История мира через призму математики

Для того чтобы понять проблематику этой дисциплины, нам снова придется погрузиться в глубь истории. Спустя 14 часов, покинув здание ЦМИ, позвольте мне проводить вас в увлекательный мир вероятностей. Случайность событий уже давно волнует умы человечества. С доисторических времен люди были свидетелями многих необъяснимых природных явлений, происходивших периодически без видимых причин. Первоначально, за неимением лучшего объяснения, эти события объяснялись волей богов. Затмения, радуга, землетрясения, эпидемии, паводки или появление комет интерпретировались как божественные послания, которые могут быть расшифрованы. Эта задача была возложена на колдунов, оракулов, священников или шаманов, которые зарабатывали на жизнь тем, что проводили многочисленные ритуалы, чтобы обратиться к богам, не дожидаясь, пока они соизволят сами проявить себя. Другими словами, люди начали искать способы влияния на наступление случайных событий.

Беломантия, или искусство гадания с помощью стрел, – это один из старейших способов принятия решения. Прикрепите к каждой из стрел один из вариантов ответа на вопрос, который вы задаете вашему богу, поместите их все в колчан, встряхните его и затем вытяните одну – это и будет ответ. Таким образом, например, поступил Навуходоносор II, царь Вавилона, когда выбирал врагов, которым он объявил войну в VI в. до н. э. Кроме стрел, выбираемые объекты могут принимать различные формы: цветные камешки, плитки, стержни или шарики. Древние римляне дали этим объектам название «жребий».

От этого слова происходит выражение «бросить жребий», а также слово «колдовство [20]», которое первоначально означало вмешательство человека в волю богов. Постепенно увеличивалось количество механизмов случайного выбора, которые приобрели множество различных форм. Жребий использовался в некоторых политических системах, таких как, например, в Афинах, чтобы выбрать пятьсот граждан, которые будут заседать в буле, или, несколько столетий спустя, в Венеции, для избрания дожей. Случайность наступления событий будет также отличным источником вдохновения для создателей игр. Так появились игра «орел или решка», игральные кости в форме Платоновых тел, а также карточные игры.

Именно благодаря появлению азартных игр, управляемых волей богов, в итоге ряд математиков заинтересовались данным вопросом. Они начали изучать вероятность наступления тех или иных случайных событий в будущем.

Все началось в середине XVII в., когда в 1635 г. математик и философ Марен Мерсенн основал Парижскую академию наук, которая впоследствии была преобразована во Французскую академию наук. Однажды в ходе дискуссии между учеными из разных слоев общества, писатель Антуан Гомбо, занимавшийся математикой в свободное время, поднял интересовавший его вопрос. Представим ситуацию, когда два игрока поставили на кон определенную сумму денег и после трех раундов счет оказался равным 2: 1 в пользу первого игрока. Если при таком счете они решают не продолжать игру, то в какой пропорции должен быть разделен игровой банк?

Среди присутствовавших в тот день ученых данным вопросом заинтересовались двое французских математиков, Пьер де Ферма и Блез Паскаль. После короткого обсуждения оба пришли к выводу, что три четверти банка должны вернуться к первому игроку, а оставшаяся четверть – ко второму. Чтобы прийти к такому выводу, ученые проанализировали все возможные сценарии развития игры, оценивая шансы каждого из игроков. Таким образом, гипотетически в следующем раунде первый игрок будет иметь 50 %-ный шанс выиграть игру, в то время как второй игрок будет иметь 50 %-ную вероятность сравнять счет. И если счет будет сравнен, в последующем раунде у игроков окажутся равные шансы на победу, т. е. вероятность каждого на победу будет равна 25 %. Можно схематично изобразить это на следующей схеме:

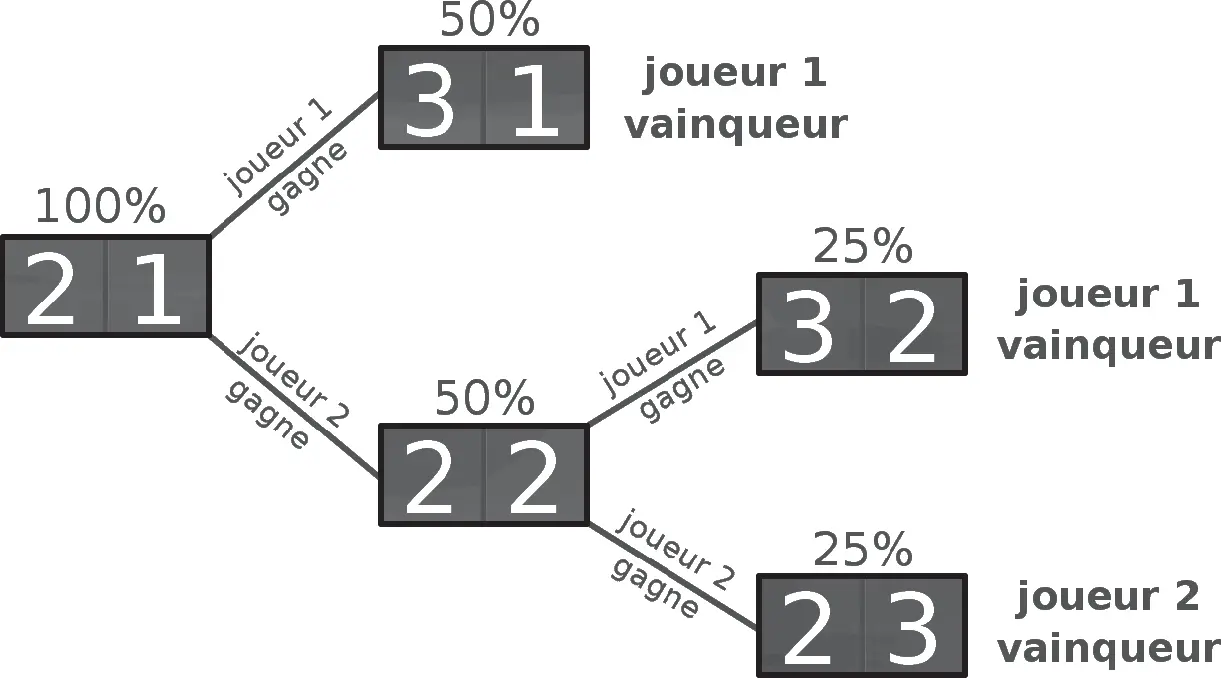
Таким образом, мы видим: вероятность победы первого игрока 75 %, второго – 25 %. Вывод, сделанный Паскалем и Ферма, заключается в том, что необходимо поделить игровой банк в соответствии с вероятностью победы: первый игрок – 75 %, а второй – оставшиеся 25 %.

Рассуждения французских ученых лягут в основу дальнейших исследований в этой области. Такой подход применим к большинству азартных игр. Швейцарский математик Якоб Бернулли был одним из первых, кто стал заниматься исследованиями в этой области и в конце XVII в. написал книгу под названием « Искусство предположений » (итал. Ars Conjectandi ), опубликованную только после его смерти в 1713 г. В этой книге он привел анализ традиционных азартных игр и впервые сформулировал один из основополагающих принципов теории вероятности: закон больших чисел.

Этот закон подтверждает, что чем больше раз будет повторяться описанный выше прием, тем более точным окажется определение вероятности, стремящееся к своему пределу. Иными словами, если продолжать эти рассуждения в долгосрочной перспективе, средние значения перестают быть случайными.

Понять это явление очень несложно. Закон больших чисел можно разобрать на примере игры «орел или решка». Если монета сбалансирована, то вероятность выпадения одной из двух сторон равна 50 %, что может быть представлено на следующей гистограмме.

Теперь представьте, что вы бросили монету два раза и затем подсчитываете общее количество выпавших орлов и решек. Возможны три варианта: два орла, две решки, орел и решка. Есть большой соблазн предположить, что вероятность наступления этих трех событий одинакова, но это не так. На самом деле вероятность выпадения орла и решки равна 50 %, а выпадения двух орлов или двух решек – по 25 % каждая.

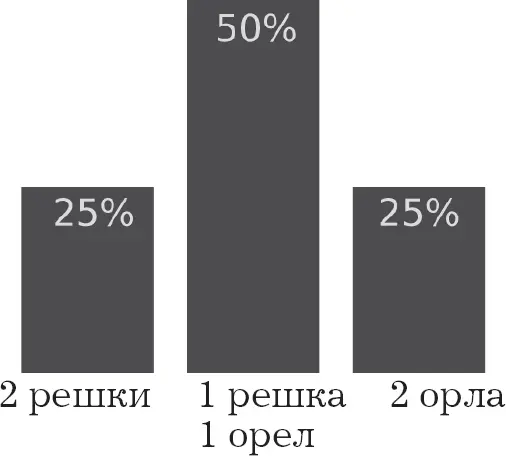
Этот дисбаланс обусловлен тем фактом, что две различные комбинации дают один и тот же конечный результат. Если дважды подбросить монету, фактически есть четыре возможных варианта: орел-орел, орел-решка, решка-орел и решка-решка. Варианты орел-решка и решка-орел дают один и тот же конечный результат: один орел и одна решка, в связи с чем вероятность выпадения такой комбинации в два раза больше. Игроки также знают, что если подбросить два игральных кубика, то выпавшая сумма будет с большей вероятностью равна 7, чем 12, потому что есть много комбинаций, сумма которых равна 7 (1 + 6, 2 + 5, 3 + 4, 4 + 3, 5 + 2 и 6 + 1) и только одна, дающая 12 (6 + 6).

Чем больше раз подбросишь монету, тем более выраженным становится это явление. Сценарии отклоняются от среднего значения, постепенно становятся исключительно редкими по сравнению со средними значениями.