Микаэль Лонэ - Большой роман о математике. История мира через призму математики

С этого момента математики начали повсеместно использовать исчисление бесконечно малых величин и применять его в решении многочисленных вопросов, возникающих в связи с тысячами физических явлений. Эта теория оказалась не просто инструментом, позволяющим решать сложные задачи, но и была удивительно красивой. Наука подобна бесконечной игре в теннис, и эти новые разработки будут постепенно находить применение в других областях, как, например, астрономия.

Бесконечно малые величины будут использоваться в решении любых задач, в которых, по аналогии с движением кометы, присутствуют непрерывно изменяющиеся величины. В метеорологии – для того чтобы моделировать и прогнозировать изменение температуры или атмосферного давления. В океанографии – чтобы следить за океаническими течениями. В аэродинамике – для контроля сопротивления воздуха с крыльями самолета или различными космическими аппаратами. В геологии – для мониторинга состояния мантии Земли и изучения вулканов, землетрясений и, в долгосрочной перспективе, дрейфа материков.

В ходе исследований математики обнаружили в бесконечно малом мире множество необычных результатов, некоторые из которых сильно озадачили их.

Одна из первых идей, как определить бесконечно малый интервал, предлагала выбрать в качестве него точку. Еще Евклид определил точку как наименьший геометрический элемент. При длине, равной 0, точка бесконечно мала. К сожалению, эта идея, такая простая в понимании, не может быть взята за основу. Для того чтобы понять это, посмотрите на этот отрезок, длина которого обозначена как 1.

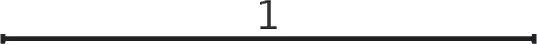
Этот отрезок состоит из бесконечного числа точек, каждая из которых имеет длину, равную 0. Так, можно сказать, что длина отрезка равна бесконечному количеству нулей! На алгебраическом языке это можно записать, как ∞ × 0 = 1, где ∞ обозначает бесконечность. Проблема этого вывода заключается в том, что если мы теперь рассмотрим отрезок, длина которого равна 2, то получится, что она тоже состоит из бесконечного числа точек, что в этот раз соответствует равенству ∞ × 0 = 2. Как может получиться так, что одинаковые расчеты приводят к двум различным результатам? Так, изменяя длину отрезка, мы можем также рассчитать, что произведение ∞ × 0 равно 3, 1000 или даже π!

Исходя из этого мы вынуждены сделать следующий вывод: используемые определения нуля и бесконечности в данном контексте недостаточно точны и не могут быть использованы в дальнейшем. Такие произведения как ∞ × 0, результат которых изменяется в зависимости от его интерпретации, называют неопределенной формой. Невозможно использовать эти формы в алгебраических вычислениях, так как мы сразу столкнемся с тысячами парадоксов! Если бы мы стали применять умножение ∞ × 0, то тем самым пришлось бы признать, что 1 равно 2 и т. д. Короче говоря, необходимо поступать иначе.

Сделаем вторую попытку. Если бесконечно малый интервал не может быть точкой, это может быть отрезок, ограниченный двумя точками, расположенными бесконечно близко друг к другу. Идея привлекательная, но мы снова сталкиваемся с проблемой, потому что таких отрезков не существует. Расстояние между двумя точками может быть сколь угодно малым, но всегда будет иметь положительную длину. Отрезки длиной в сантиметр, миллиметр, одну миллиардную миллиметра или даже меньше, конечно, очень малы, но ни в коем случае не бесконечно малы. Иными словами, две точки никогда не будут соприкасаться.

Есть что-то очень обескураживающее в этом заявлении. Когда вы рисуете непрерывную линию, например отрезок, в ней нет никаких промежутков, и тем не менее точки, которые составляют ее, не соприкасаются! Ни одна точка не соприкасается с другими. Отсутствие отверстий в линии является всего лишь следствием того, что она состоит из бесконечно малых точек. И если определять точки линии по их взаимосвязям, это же явление можно представить в алгебраической форме следующим образом: два различных числа никогда не идут подряд, всегда есть бесконечное множество других чисел, которые находятся между ними. Между числами 1 и 2 находится 1,5. Между числами 1 и 1,1 находится 1,05. А между числами 1 и 1,0001 есть 1,00005. Так можно продолжать до бесконечности. С числом 1, как и со всеми другими, не «соприкасаются» другие числа. Однако бесконечная совокупность бо́льших и меньших чисел обеспечивает непрерывность последовательности.

После двух неудачных попыток нам приходится признать, что во множестве классических чисел по определению невозможно выделить бесконечно малые величины. Эти неуловимые числа не могут быть приравнены к нулю и также меньше всех существующих положительных чисел, поэтому придется отдельно описывать их с самого начала! Над этим работали Лейбниц и ученые, которые последовали его примеру в исчисления бесконечно малых величин. Потребовалось три столетия для того, чтобы сформулировать правила расчета, которые применяются к этим новым числам, и определить сферу их действия. Таким образом, с XVII по XX в. был разработан целый арсенал теорем, позволяющих эффективно решать задачи с бесконечно малыми величинами.

Числа, которые не существуют в действительности, тем не менее могут быть использованы в качестве промежуточного результата? Это вам ничего не напоминает? Так уже было с отрицательными и мнимыми числами. Но, как это часто бывает, процесс внедрения длится долго и не всегда можно предсказать исход. В 1960-е годы американский математик Абрахам Робинсон разработал новую модель, в которой бесконечно малые величины рассматривались как отдельная группа чисел. Тем не менее в отличие от мнимых чисел, бесконечно малые величины и сегодня, в начале XXI в., фактически не относят к действительным числам. Нестандартная модель анализа Робинсона вызывает множество противоречий и редко используется на практике.

Возможно, в будущем нас неизбежно ждут открытия, исследования, теоремы, созданные на основе этой нестандартной теории. А может быть, наоборот, у нее нет потенциала, чтобы стать доминирующей моделью, и бесконечно малые величины никогда не сравнятся по значимости со своими прославленными предшественниками – отрицательными и мнимыми числами. Нестандартный анализ, безусловно, интересен, но, возможно, несет в себе слишком мало пользы, чтобы продолжительное время поддерживать энтузиазм. Прошло всего несколько десятилетий с момента разработки Робинсоном своей модели, и математикам будущего еще предстоит решить ее судьбу.

Среди наиболее успешных разработок исчисления бесконечно малых величин можно выделить теорию меры, разработанную в начале XX в. французским математиком Анри Леоном Лебегом – одно из самых любопытных направлений. Возникает вопрос: можно ли с использованием бесконечно малых величин создать новые геометрические фигуры, которые нельзя нарисовать с помощью циркуля и линейки. Ответ: да, и эти новые фигуры будут созданы в течение нескольких лет в соответствии с законами классической геометрии. Возьмем, например, отрезок, размеченный от 0 до 10.