РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров

где N = число «ног» позиции;

HPR(T, U) = HPR для данного тестируемого значения Т и U;

С. (Т, U) = коэффициент i-ой «ноги» при данном значении U, когда время, оставшееся до истечения срока, равно Т.

Для опционных «ног», занесенных в дебет, или длинной позиции по базовому инструменту:

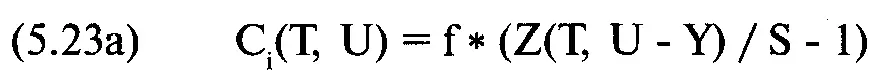
Для опционных «ног», занесенных в кредит, или короткой позиции по базовому инструменту:

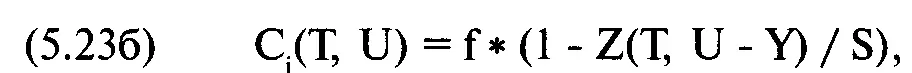
где f = тестируемое значение f;

S = текущая цена опциона;

Z(T, U - Y) = теоретическая цена опциона, когда цена базового инстру­мента равна U - Y, а время, оставшееся до срока истечения, равно Т;

P j(T, U) = вероятность того, что базовый инструмент равен U, когда время, оставшееся до истечения срока исполне­ния, равно Т;

Y = разность между арифметическим математическим ожи­данием базового инструмента (согласно уравнению (5.10)) и текущей ценой.

Теперь мы можем рассчитать среднее геометрическое HPR для случайной связи:

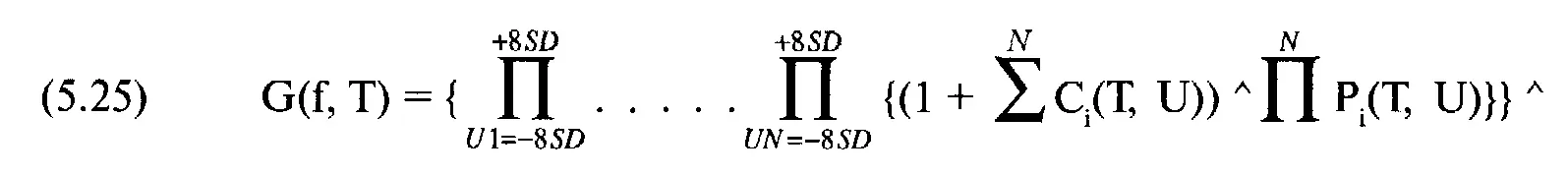
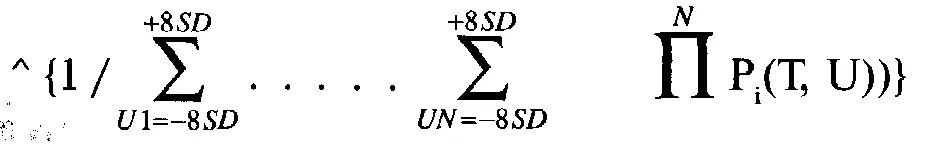
где G(f, Т) = среднее геометрическое HPR для данного тестируе­мого значения f и данного времени Т, остающегося до истечения срока от указанной даты выхода. Зна­чения f и Т, которые дают наибольшее среднее геометрическое, оптимальны. Структура этой процедуры такая же, как и в случае с причинной связью:

Для каждой даты выхода между текущей датой и датой истечения

Для каждого значения f (пока не будет найдено оптимальное)

Для каждой рыночной системы

Для каждого тика между +8 и -8 стандартными отклонениями

Определите HPR

Единственное различие между процедурой нахождения среднего геометрического для случайных связей и процедурой для причинных связей состоит в том, что пока­затель степени для каждого HPR при случайной связи рассчитывается путем умно­жения вероятностей того, что «ноги» будут находиться на данной цене определен­ного HPR. Все эти суммы вероятностей, используемые в качестве показателей сте­пени для каждого HPR, сами по себе также суммируются, так что, когда все HPR перемножены для получения промежуточного TWR, его можно возвести в степень единицы, деленной на сумму показателей степени, используемых в HPR. И снова процедуру можно изменить, чтобы найти оптимальные даты выхода для каждой составляющей позиции.

Несмотря на всю сложность, уравнение (5.25) все-таки не решает проблему ненулевого коэффициента линейной корреляции между ценами двух компо­нентов. Как видите, определение оптимальных весов компонентов является до­вольно сложной задачей! В следующих нескольких главах вы увидите, как найти правильные веса для каждой составляющей позиции, будь то акция, товар, опцион или любой другой инструмент, независимо от связи (причинная, случай­ная или корреляционная). Входные данные, которые нам потребуются, следую­щие: (1) коэффициенты корреляции средних дневных HPR позиций в портфеле на основе 1 контракта, (2) арифметические среднее HPR и стандартные откло­нения HPR.

Уравнения (5.14) и (5.20) показывают, как находить HPR для длинных и коротких позиций по опционам. Уравнение (5.18) показывает, как находить среднее геометри­ческое. Мы можем также определить среднее арифметическое:

Для длинных опционных позиций, т.е. отнесенных в дебет:

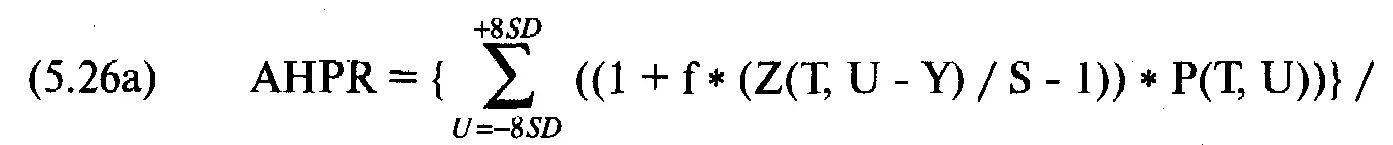
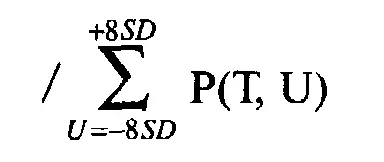
Для коротких опционных позиций, т.е. отнесенных в кредит:

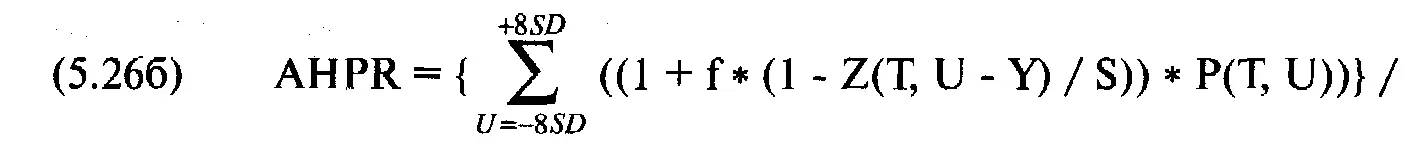
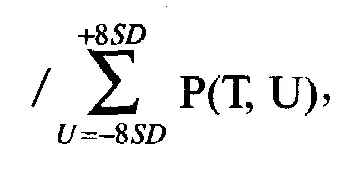
где AHPR = среднее арифметическое HPR;

f= оптимальное f (от 0 до 1);

S= текущая цена опциона;

Z(T, U - Y)= теоретическая цена опциона, когда цена базового инстру­мента равна U - Y, а время, оставшееся до срока истечения, равно Т;

Р(Т, U) = вероятность, что базовый инструмент равен U, когда время, ос­тавшееся до истечения срока исполнения, равно Т;

Y= разность между арифметическим математическим ожидани­ем базового инструмента (согласно уравнению (5.10)) и теку­щей ценой.

Зная среднее геометрическое HPR и среднее арифметическое HPR, можно опре­делить стандартное отклонение значений HPR:

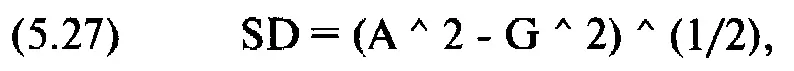
где А = арифметическое среднее HPR;

G = геометрическое среднее HPR;

SD = стандартное отклонение значений HPR.

В этой главе мы познакомились еще с одним способом расчета оптимального f. Предложенный метод подходит для несистемных трейдеров. В виде входного па­раметра здесь используется распределение результатов по базовому инструменту к определенной дате в будущем. Данный подход позволяет найти оптимальное f как для отдельных опционных позиций, так и для сложных позиций. Существен­ным недостатком метода является то, что связи между всеми позициями должны быть случайными или причинными.

Означает ли вышесказанное, что мы не можем использовать методы поиска оптимального f, рассмотренные в предыдущих главах, для нескольких одновре­менно открытых позиций или опционов? Нет, вы всегда можете выбрать наиболее эффективный с вашей точки зрения подход. Методы, детально описанные в этой главе, имеют как определенные недостатки, так и достоинства (например воз­можность расчета оптимального времени выхода). В следующей главе мы будем изучать темы, касающиеся построения оптимального портфеля, что позднее по­может нам в управлении капиталом при одновременной торговле по нескольким позициям.

Цель этой книги — изучить портфели рыночных систем, использующих раз­личные инструменты с различных рынков. В данной главе мы достаточно подроб­но рассмотрели теоретические цены опционов и теперь перейдем к созданию оп­тимального портфеля.

Глава 6

Корреляционные связи и выведение эффективной границы

Мы узнали несколько способов поиска оптимального количества при торговле фьючерсами, акциями и опционами (по отдельнос­ти или совместно с другими инструментами), когда существует либо случайная, либо причинная связь между ценами инструмен­тов. Можно определить оптимальный набор, когда коэффици­ент линейной корреляции двух любых элементов портфеля равен 1, - 1 или 0. Однако связи между двумя элементами портфеля, рассматриваем ли мы корреляцию цен (в немеханической торго­вой системе) или изменений баланса (в механической системе), редко дают такие удобные значения коэффициентов линейной корреляции. В этой главе описан способ определения эффективной границы портфелей рыночных систем, когда коэффициенты линейной кор­реляции любых двух компонентов рассматриваемого портфеля принимают произвольные значения между -1 и 1 включительно. Далее описан метод, применяемый профессионалами для расчета оптимальных портфелей акций. В следующей главе мы адаптируем его для использования любых инструментов. Данная глава основана на важном предположении, которое зак­лючается в том, что распределения, генерирующие последова­тельность сделок (распределения прибылей), имеют конечную дисперсию. Предложенные методы эффективны только тогда, когда используемые входные данные имеют конечную дисперсию [24] Для получения дополнительной информации прочитайте Fama, Eugene E, «Portfolio Analysis in a Stable Paretian Market», Management Science 11, pp. 404 — 419, 1965. Фама продемонстрировал параметрические методы поиска эффектив­ной границы для стабильно распределенных ценных бумаг (распределения которых обладают одинаковым характеристическим показателем А), когда прибыли компонен­тов зависят от одного индекса основного рынка. Существует и другая работа, посвя­щенная выведению эффективной границы в условиях бесконечной дисперсии прибы­лей компонентов портфеля. Эти методы не рассматриваются в данной книге, но для заинтересованных читателей есть ссылки на соответствующие статьи. О распределении Парето вы сможете узнать из приложения В. Несколько слов о бесконечной дисперсии сказано в разделе «Распределение Стьюдента» в приложении В. .