РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров
- Название:Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров
- Автор:
- Жанр:
- Издательство:Альпина Паблишер
- Год:2007
- ISBN:ISBN 978-5-9614-0610-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров краткое содержание
Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
| I | L | S | |
| Т | -0,15 | 0,05 | о |
| I | 0,25 | о | |
| L | о | ||
На основе полученных параметров мы можем рассчитать ковариацию между двумя ценными бумагами:

Стандартные отклонения S aи S бможно найти, взяв квадратный корень дисперсии ожидаемых прибылей для ценных бумаг а и б. Вернемся к нашему примеру. Мы можем определить ковариацию между Toxico (Т) и Incubeast (I) следующим образом:

Зная ковариацию и стандартные отклонения, мы можем рассчитать коэффициент линейной корреляции:

Отметьте, что ковариация ценной бумаги самой к себе является дисперсией, так как коэффициент линейной корреляции ценной бумаги самой к себе равен 1:

Теперь можно создать таблицу ковариаций для нашего примера с четырьмя инвестиционными альтернативами:
| Т | I | L | S | |
| Т | 0,1 | - 0,0237 | 0,01 | 0 |
| I | - 0,0237 | 0,25 | 0,079 | 0 |
| L | 0,01 | 0,079 | 0,4 | 0 |
| S | 0 | 0 | 0 | 0 |
Мы собрали необходимую параметрическую информацию и теперь попытаемся сформулировать основную проблему. Во-первых, сумма весов ценных бумаг, составляющих портфель, должна быть равна 1, так как операции ведутся на денежном счете, и каждая ценная бумага полностью оплачена:
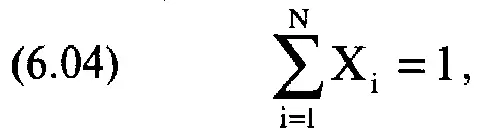
где N == число ценных бумаг, составляющих портфель;
Х = процентный вес ценной бумаги L
Важно отметить, что в уравнении (6.04) каждое значение Х должно быть неотрицательным числом.
Следующее равенство относится к ожидаемой прибыли всего портфеля — это Е в теории Е — V. Ожидаемая прибыль портфеля является суммой прибылей его компонентов, умноженных на соответствующие веса:
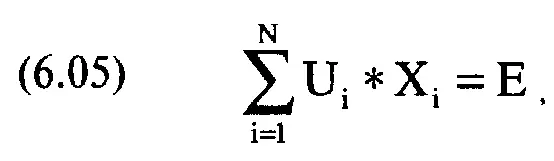
где Е = ожидаемая прибыль портфеля;
N = число ценных бумаг, составляющих портфель;
X i= процентный вес ценной бумаги i;
U i= ожидаемая прибыль ценной бумаги i. И наконец, мы подошли к параметру V, т. е дисперсии ожидаемых прибылей:
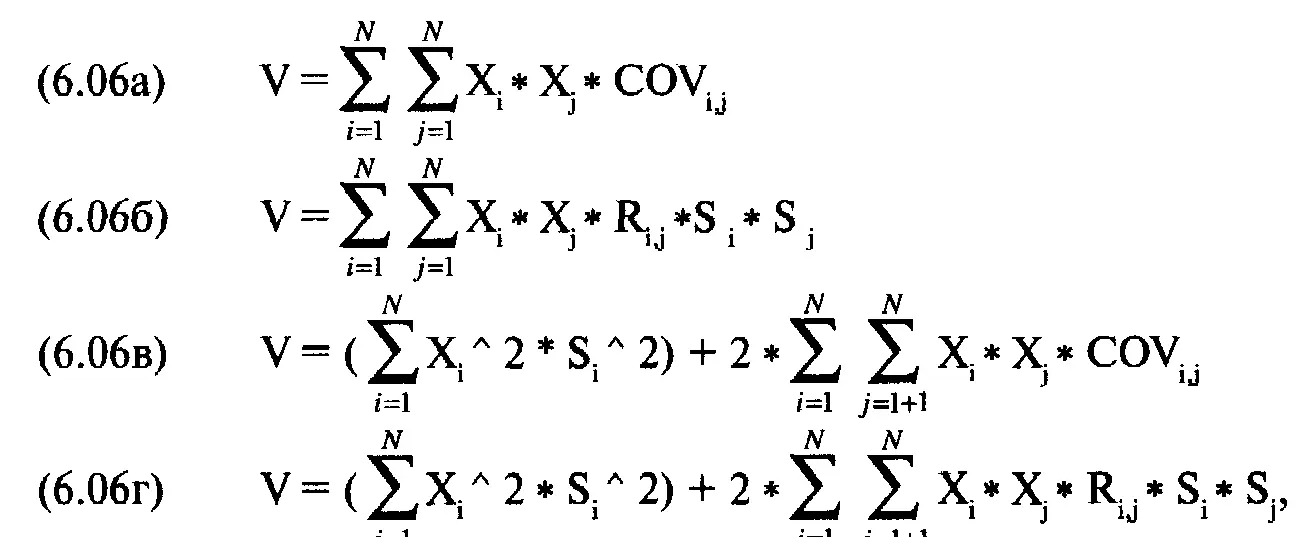

Нашей целью является поиск значений Х (причем их сумма равна единице), которые дают наименьшее значение V для определенного значения Е. Максимизировать (или минимизировать) функцию Н(Х, Y) при наличии условия или ограничения G(X, Y) можно с помощью метода Лагранжа. Для этого зададим функцию Лагранжа F(X, Y, L):
(6.07) F(X,Y,L) = H(X,Y) + L * G(X,Y)
Обратите внимание на форму уравнения (6.07). Новая функция F(X,Y,L) равна множителю Лагранжа L (его значение мы пока не знаем), умноженному на ограничительную функцию G(X,Y), плюс первоначальная функция H(X,Y), экстремум которой мы и хотим найти.
Решение этой системы из трех уравнений даст точки (X 1Y 1) относительного экстремума:
F xX,Y,L) = О F y(X,Y,L) = О F L(X,Y,L) = О
Допустим, мы хотим максимизировать произведение двух чисел при условии, что их сумма равна 20. Пусть Х и Y два числа. Таким образом, H(X,Y) = Х * Y является функцией, которая должна быть максимизирована при наличии ограничительной функции G(X,Y) = Х + Y - 20 = 0. Зададим функцию Лагранжа:
F(X,Y,L) = Х * Y + L * (X + Y- 20) F x(X,Y,L)=Y+L F y(X,Y,L)=X+L F L(X,Y,L)=
X +Y-20
Теперь приравняем F^(X,Y,L) и Fy(X,Y,L) нулю и решим каждое из них для получения L:
Y+L=0 Y=-L и
X+L=0 X=-L
Теперь, приняв F L(X,Y,L) = 0, мы получим Х + Y - 20 = 0. Наконец, заменим Х и Y эквивалентными выражениями, содержащими L:
(-L) + (-L) - 20 = О 2 * -L - 20 L=-10
Так как Y = -L, то Y = 10 и Х = 10. Максимальное произведение: 10*10= 100.
Метод множителей Лагранжа был продемонстрирован для двух переменных и одной 01раничительной функции. Метод можно также применять, когда есть более чем две переменные и более чем одна ограничительная функция. Далее для примера следует форма для поиска экстремума, когда есть три переменные и две ограничительные функции:
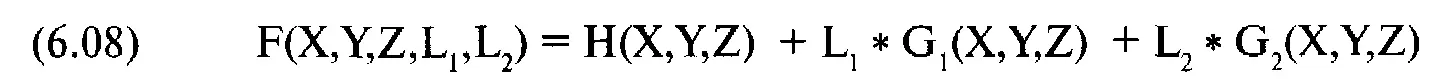
В этом случае, чтобы определить точки относительных экстремумов, вам надо решить систему из пяти уравнений с пятью неизвестными. Позже мы покажем, как это сделать.
Сформулируем проблему несколько иначе: необходимо минимизировать V, т.е. дисперсию всего портфеля, с учетом двух следующих ограничений:
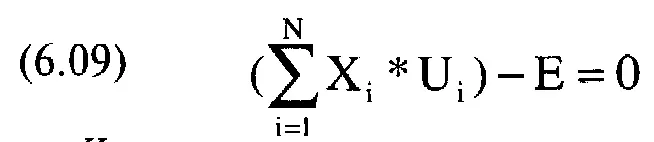
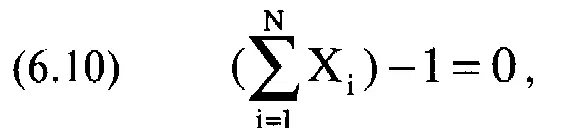
где N= число ценных бумаг, составляющих портфель;
Е = ожидаемая прибыль портфеля;
Х = процентный вес ценной бумаги i;
U. = ожидаемая прибыль ценной бумаги i.
Минимизация ограниченной функции многих переменных может быть проведена путем введения множителей Лагранжа и частного дифференцирования по каждой переменной. Поэтому мы сформулируем поставленную задачу в терминах функции Лагранжа, которую назовем Т:
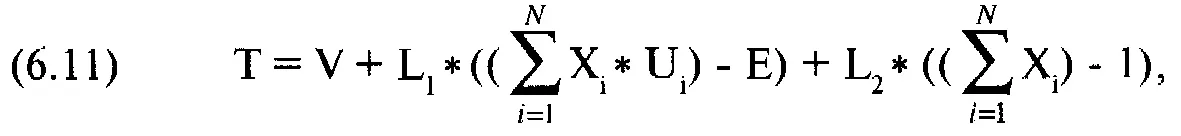
где V= дисперсия ожидаемых прибылей портфеля из уравнения (6.06);
N = число ценных бумаг, составляющих портфель;
Е = ожидаемая прибыль портфеля;
X. = процентный вес ценной бумаги i;
U. = ожидаемая прибыль ценной бумаги i;
L, = первый множитель Лагранжа;
L = второй множитель Лагранжа.
Мы получим портфель с минимальной дисперсией (т.е. минимальным риском), приравняв к нулю частные производные функции Т по всем переменньм.
Давайте снова вернемся к нашим четырем инвестициям: Toxico, Incubeast Corp., LA Garb и сберегательному счету. Если мы возьмем первую частную производную Т по Х 1, то получим:
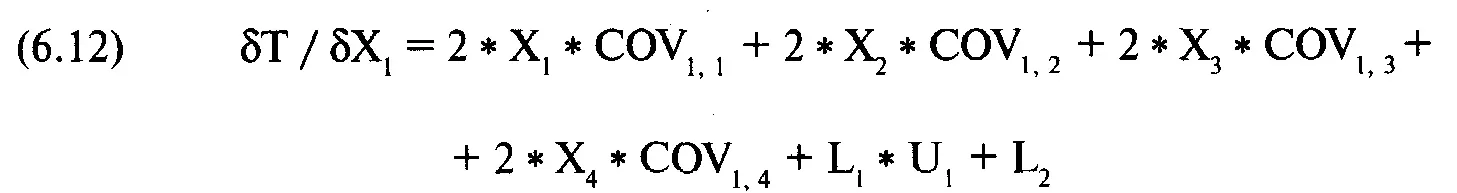
Интервал:
Закладка:










