РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров
- Название:Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров
- Автор:
- Жанр:
- Издательство:Альпина Паблишер
- Год:2007
- ISBN:ISBN 978-5-9614-0610-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров краткое содержание
Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Приравняв это выражение нулю и разделив обе части уравнения на 2, получим:
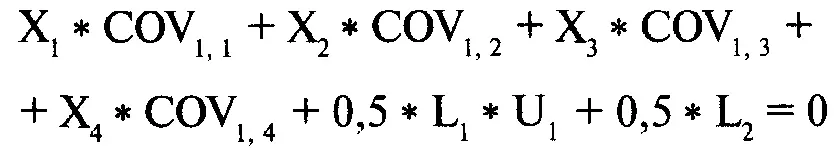
Таким же образом:
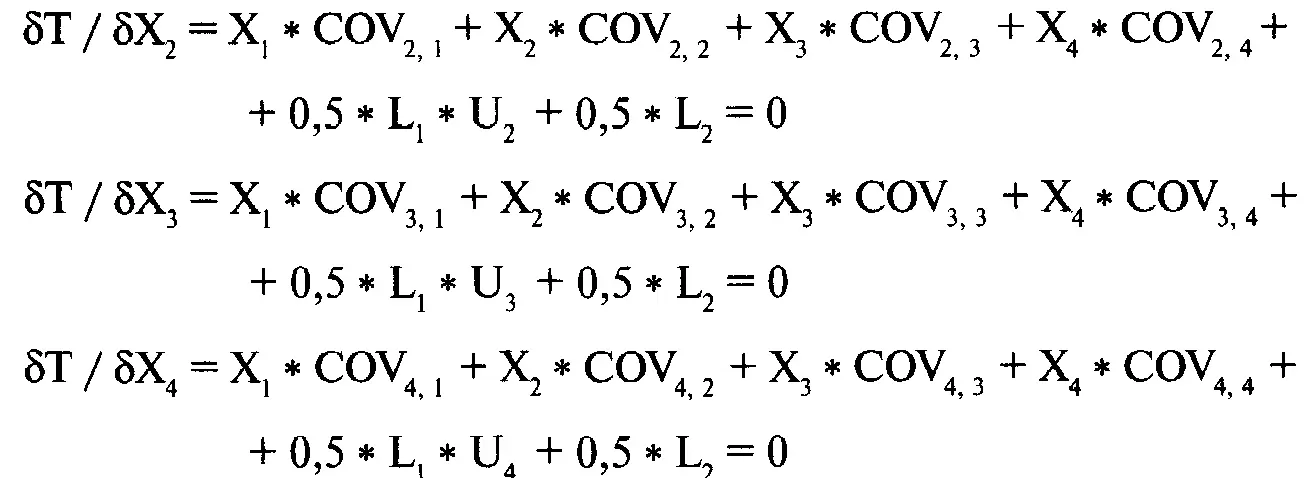
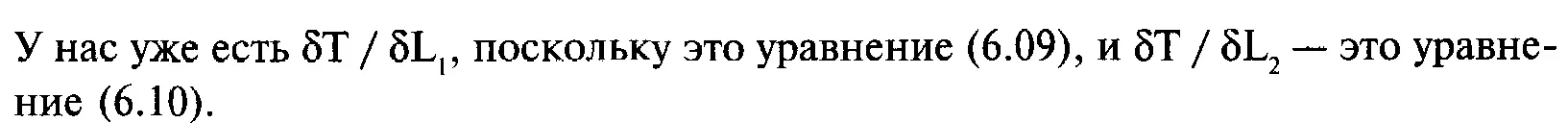
Таким образом, проблему минимизации V при данном Е для портфеля с N компонентами можно решить с помощью системы N + 2 уравнений с N + 2 неизвестными. Для случая с четырьмя компонентами обобщенная форма будет иметь следующий вид:
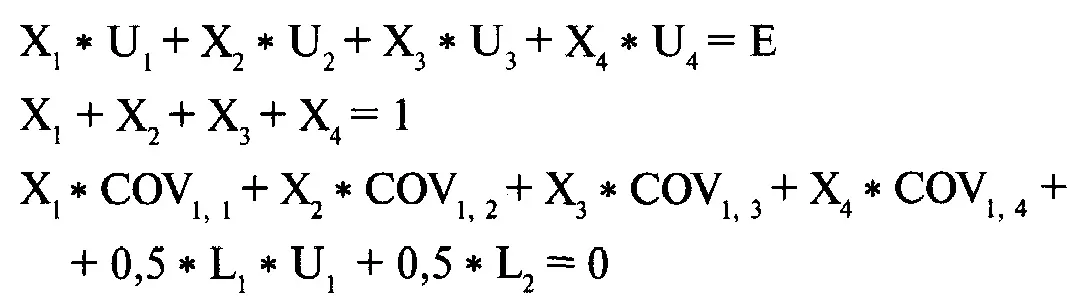
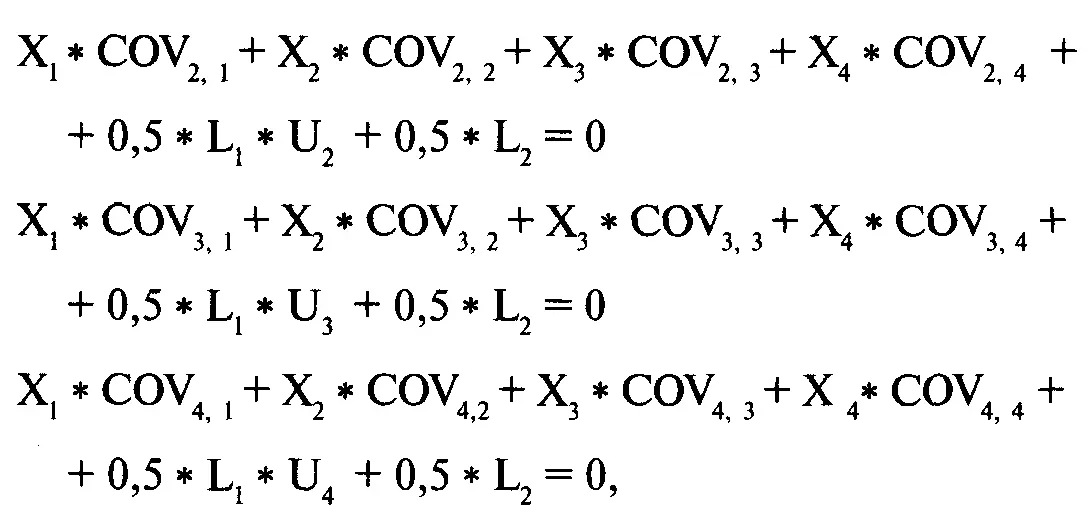
где Е = ожидаемая прибыль портфеля;
Х i= процентный вес ценной бумаги i;
U i= ожидаемая прибыль по ценной бумаге i;
COV А, Б= ковариация между ценными бумагами А и Б;
L 1= первый множитель Лагранжа;
1 2= второй множитель Лагранжа.
Обобщенную форму можно использовать для любого числа компонентов. Например, если речь идет о трех компонентах (т.е. N = 3), система уравнений будет выглядеть следующим образом:
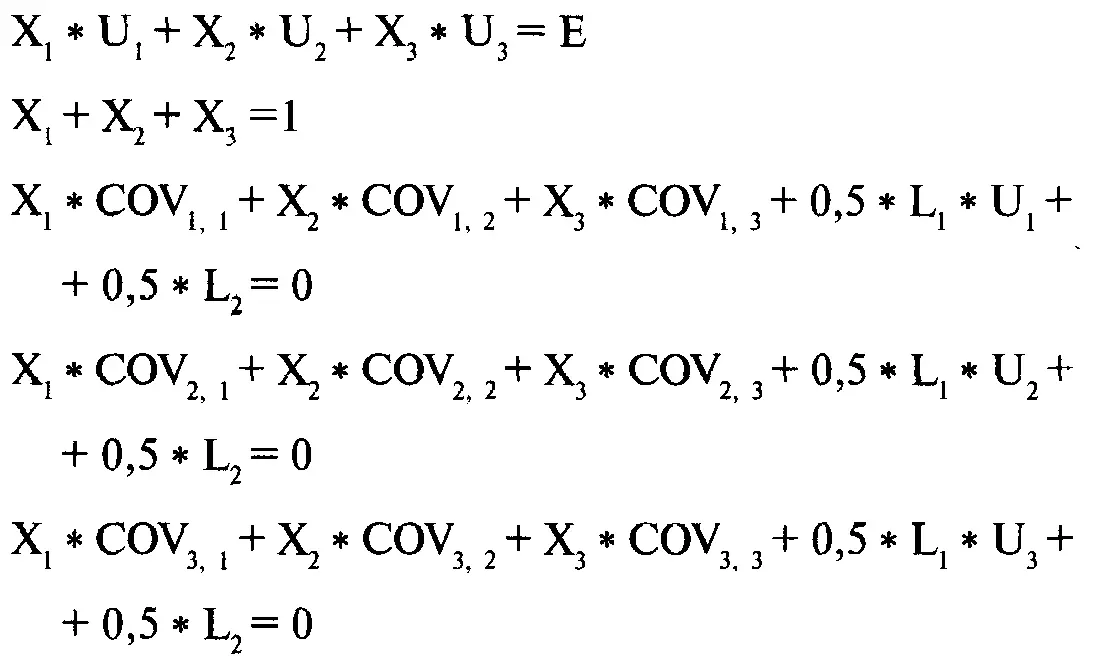
Прежде чем решать систему уравнений, необходимо задать уровень ожидаемой прибыли Е. Решением будет комбинация весов, которая даст искомое Е при наименьшей дисперсии. После того как вы определитесь с выбором Е, у вас будут все входные переменные, необходимые для построения матрицы коэффициентов.
Переменная Е в правой части первого уравнения — это значение прибыли. для которой вы хотите определить комбинацию ценных бумаг в портфеле. Первое уравнение говорит о том, что сумма всех ожидаемых прибылей, умноженных на
соответствующие веса, должна равняться заданному Е. Второе уравнение отражает тот факт, что сумма весов должна быть равна 1. Была показана матрица для случая с тремя ценными бумагами, но вы можете использовать обобщенную форму для N ценных бумаг.
Возьмем ожидаемые прибыли и ковариации из уже известной таблицы ковариаций и подставим коэффициенты в обобщенную форму. Таким образом из коэффициентов обобщенной формы можно создать матрицу. В случае четырех компонентов (N = 4) мы получим 6 рядов (N + 2):
| X 1 | X 2 | X 3 | X 4 | L 1 | L 2 | Ответ |
| 0,095 | 0,13 | 0,21 | 0,085 | Е | ||
| 1 | 1 | 1 | 1 | 1 | ||
| 0,1 | - 0,0237 | 0,01 | 0 | 0,095 | 1 | 0 |
| - 0,0237 | 0,25 | 0,079 | 0 | 0,13 | 1 | 0 |
| 0,01 | 0,079 | 0,4 | 0 | 0,21 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0,085 | 1 | 0 |
Отметьте, что мы получили 6 столбцов коэффициентов. Если добавить столбец свободных членов к матрице коэффициентов, мы получим расширенную матрицу.
Заметьте, что коэффициенты в матрице соответствуют нашей обобщенной форме:
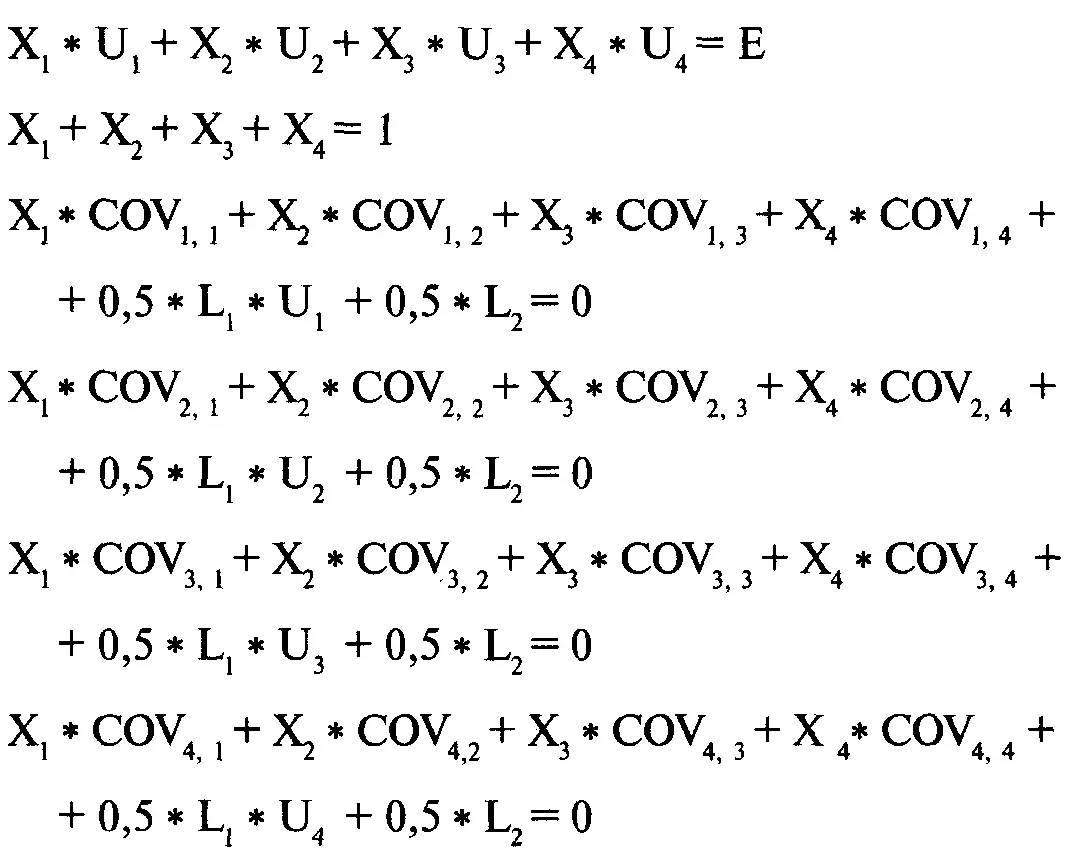
Матрица является удобным представлением этих уравнений. Чтобы решить систему уравнений, необходимо задать Е. Ответы, полученные при решении этой
системы уравнений, дадут оптимальные веса, минимизирующие дисперсию прибыли всего портфеля для выбранного уровня Е.
Допустим, мы хотим найти решение для Е = 0,14, что соответствует прибыли в 14%. Подставив в матрицу 0,14 для Е и нули для переменных L 1и L 2в первых двух строках, мы получим следующую матрицу:
| X 1 | X 2 | Х 3 | X 4 | L 1 | L 2 | Ответ |
| 0,095 | 0,13 | 0,21 | 0,085 | 0 | 0 | 0,14 |
| 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 0,1 | - 0,0237 | 0,01 | 0 | 0,095 | 1 | 0 |
| - 0,0237 | 0,25 | 0,079 | 0 | 0,13 | 1 | 0 |
| 0,01 | 0,079 | 0,4 | 0 | 0,21 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0,085 | 1 | 0 |
Необходимо найти N + 2 неизвестных с помощью N + 2 уравнений.
Решение систем линейных уравнений с использованием матриц-строк.
Многочлен — это алгебраическое выражение, которое является суммой определенного количества элементов. Многочлен с одним элементом называется одночленом, с двумя элементами — двучленом, с тремя — трехчленом и т.д. Выражение 4 * А ^ 3 + А ^ 2 +А+2 является многочленом, имеющим четыре члена. Члены отделены знаком (+).
Многочлены имеют различные степени. Степень многочлена определяется значением наибольшей степени любого из элементов. Степенью элемента является сумма показателей переменных, содержащихся в элементе. Показанное выше выражение является многочленом третьей степени, так как элемент 4 * А^ 3 имеет третью степень, и это наивысшая степень среди всех элементов многочлена. Если бы элемент был равен 4*A^З*B^62*C, мы бы получили многочлен шестой степени, так как сумма показателей переменных (3+2+1) равна 6.
Многочлен первой степени называется также линейным уравнением и графически задается прямой линией. Многочлен второй степени называется квадратным уравнением и на графике представляет собой параболу. Многочлены третьей, четвертой и пятой степени называются соответственно кубическим уравнением, уравнением четвертой степени, уравнением пятой степени и т.д. Графики многочленов третьей степени и выше довольно сложны. Многочлены могут иметь любое число элементов и любую степень, мы будем работать только с линейными уравнениями, т.е. многочленами первой степени. Решить систему линейных уравнений можно с помощью процедуры Гаусса-Жордана, или, что то же самое, метода гауссовского исключения. Чтобы использовать этот метод, мы должны сначала создать расширенную матрицу, объединив матрицу коэффициентов и столбец свободных членов. Затем следует произвести элементарные преобразования для получения единичной матрицы. С помощью элементарных преобразований мы получаем более простую, но эквивалентную первоначальной, матрицу. Элементарные преобразования производятся посредством построчных операций (мы опишем их ниже). Единичная матрица является квадратной матрицей коэффициентов, где все элементы равны нулю, кроме диагональной линии элементов, которая начинается в верхнем левом углу. Для матрицы коэффициентов «шесть на шесть» единичная матрица будет выглядеть следующим образом:
Читать дальшеИнтервал:
Закладка:










