РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров
- Название:Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров
- Автор:
- Жанр:
- Издательство:Альпина Паблишер
- Год:2007
- ISBN:ISBN 978-5-9614-0610-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров краткое содержание
Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:

Подставим значения в уравнение (6.06a) (стр. 281):
Таким образом, при Е = 0,14 самое низкое значение V = 0,0725872809.
Если мы захотим протестировать значение Е = 0,18, то снова начнем с расширенной матрицы, только на этот раз правая верхняя ячейка будет равна 0.18.
| X i | X j | COV i, j | |||
| 0,12391 | * | 0,12391 | * | 0,1 | 0,0015353688 |
| 0,12391 | * | 0,12787 | * | -0,0237 | -0,0003755116 |
| 0,12391 | * | 0,38407 | * | 0,01 | 0,0004759011 |
| 0,12391 | * | 0,36424 | * | 0 | 0 |
| 0,12787 | * | 0,12391 | * | -0,0237 | -0,0003755116 |
| 0,12787 | * | 0,12787 | * | 0,25 | 0,0040876842 |
| 0,12787 | * | 0,38407 | * | 0,079 | 0,0038797714 |
| 0,12787 | * | 0,36424 | * | 0 | 0 |
| 0,38407 | * | 0,12391 | * | 0,01 | 0,0004759011 |
| 0,38407 | * | 0,12787 | * | 0,079 | 0,0038797714 |
| 0,38407 | * | 0,38407 | * | 0,4 | 0,059003906 |
| 0,38407 | * | 0,36424 | * | 0 | 0 |
| 0,36424 | * | 0,12391 | * | 0 | 0 |
| 0,36424 | * | 0,12787 | * | 0 | 0 |
| 0,36424 | * | 0,38407 | * | 0 | 0 |
| 0,36424 | * | 0,36424 | * | 0 | 0 |
| 0,0725872809 | |||||
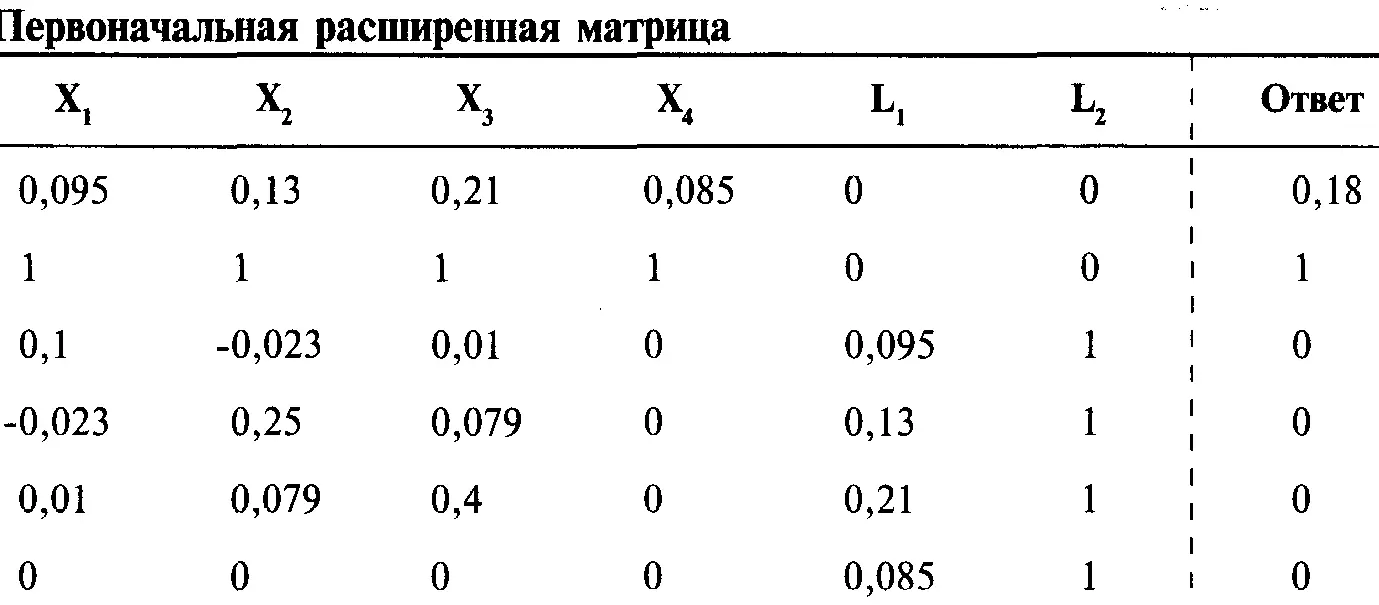
С помощью построчных операций получим единичную матрицу:

На этот раз в четвертой ячейке столбца ответов мы получили отрицательный результат. Это означает, что нам следует инвестировать отрицательную сумму в размере 9,81% капитала в сберегательный счет. Чтобы решить проблему отрицательного X i(т.е. когда значение на пересечении строки i и крайнего правого столбца меньшее или равно нулю), мы должны удалить из первоначальной расширенной матрицы строку i + 2 и столбец i и решить задачу для новой расширенной матрицы. Если значения последних двух строк крайнего правого столбца меньше или равны нулю, нам не о чем беспокоиться, поскольку они соответствуют множителям Лагранжа и могут принимать отрицательные значения. Так как отрицательное значение переменной соответствует отрицательному весу четвертого компонента, мы удалим из первоначальной расширенной матрицы четвертый столбец и шестую строку. Затем используем построчные операции для проведения элементарных преобразований, чтобы получить единичную матрицу:
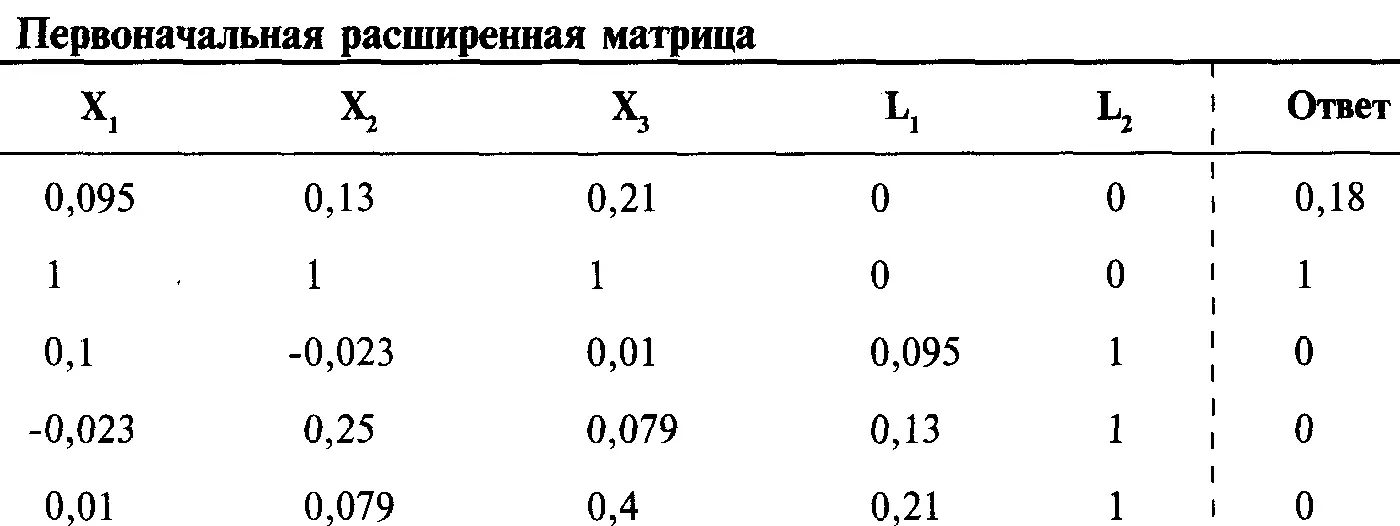
С помощью построчных операций получим единичную матрицу:

Когда вы удаляете строки и столбцы, важно помнить, какие строки каким переменным соответствуют, особенно когда таких строк и столбцов несколько. Допустим, нам надо найти веса в портфеле при Е = 0,1965. Единичная матрица, которую мы сначала получим, будет содержать отрицательные значения для весов Toxico (X 1) и сберегательного счета (Х 4). Поэтому вернемся к нашей первоначальной расширенной матрице:
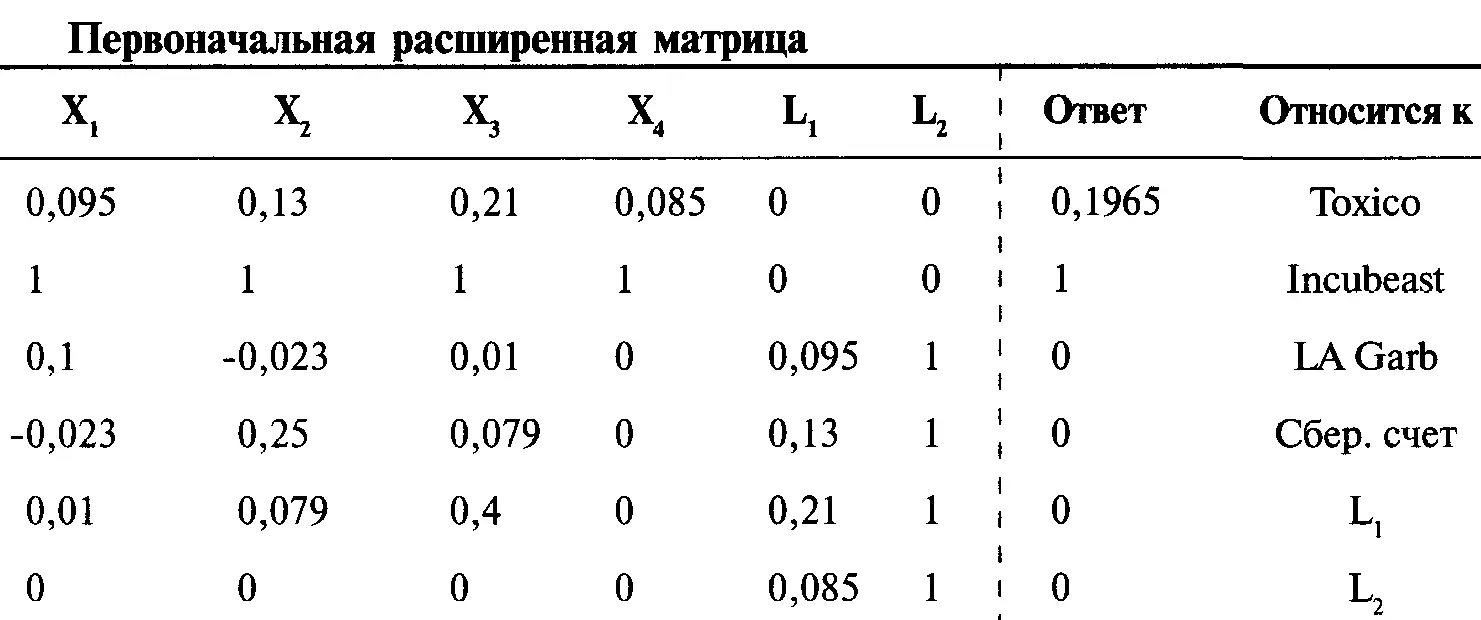
Теперь удалим строку 3 и столбец 1 (они относятся к Toxico), а также удалим строку 6 и столбец 4 (они относятся к сберегательному счету):

Итак, мы будем работать со следующей матрицей:

С помощью построчных операций получим единичную матрицу:
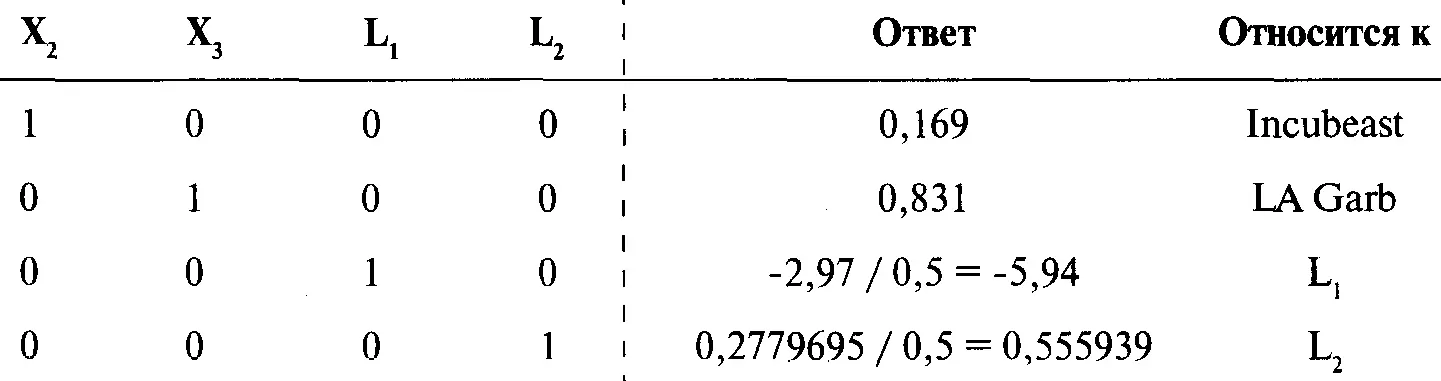
Решить матрицу можно также с помощью обратной матрицы коэффициентов. Обратная матрица при умножении на первоначальную матрицу дает единичную матрицу. В матричной алгебре матрица часто обозначается выделенной заглавной буквой. Например, мы можем обозначить матрицу коэффициентов буквой С. Обратная матрица помечается верхним индексом -1. Обратная матрица к С обозначается как С -1.Чтобы использовать этот метод, необходимо определить обратную матрицу для матрицы коэффициентов. Для этого добавим к матрице коэффициентов единичную матрицу. В примере с 4 акциями:
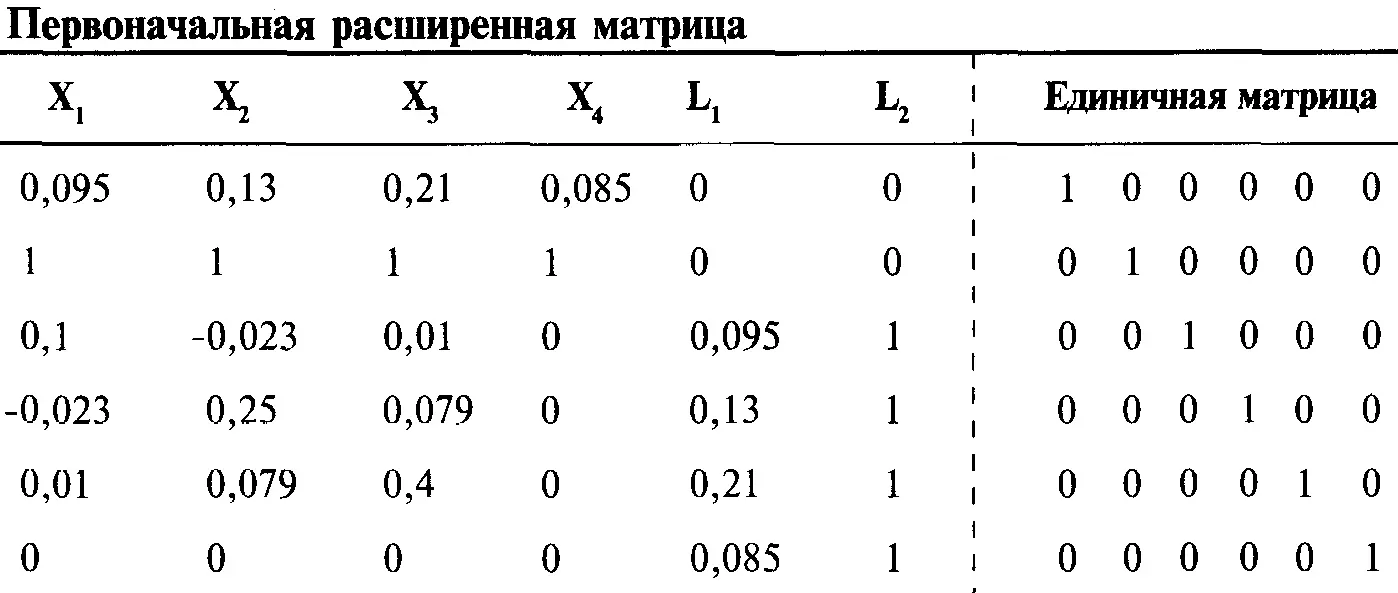
Используя построчные операции, преобразуем матрицу коэффициентов в единичную матрицу. Так как каждая построчная операция, проведенная слева, будет проведена и справа, мы преобразуем единичную матрицу справа в обратную матрицу С -1.
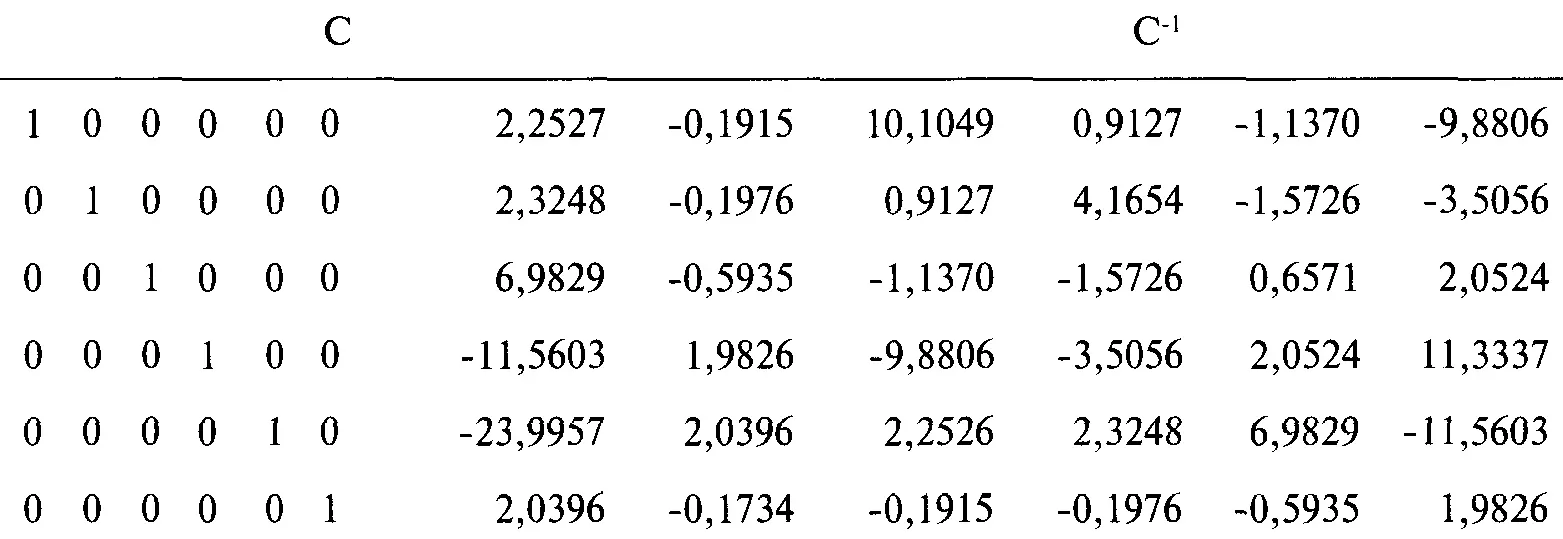
Теперь мы можем умножить обратную матрицу С -1на первоначальный крайний правый столбец, который в нашем случае выглядит следующим образом:
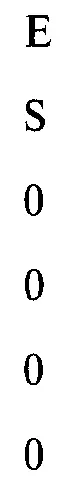
При умножении матрицы на вектор-столбец мы умножаем все элементы первого столбца матрицы на первый элемент вектора, все элементы второго столбца матрицы на второй элемент вектора, и так далее. Если бы вектор был вектор-строка, мы бы умножили все элементы первой строки матрицы на первый элемент вектора, все элементы второй строки матрицы на второй элемент вектора, и так далее. Так как речь идет о векторе-столбце и последние четыре элемента нули, нам надо умножить первый столбец обратной матрицы на Е (ожидаемая прибыль портфеля) и второй столбец обратной матрицы на S (сумма весов). Мы получим следующий набор уравнений, в которые можно подставить значения Е и S и получить оптимальные веса.
Матричная алгебра включает в себя гораздо больше тем и приложений, чем было рассмотрено в этой главе. Существуют и другие методы матричной алгебры для решения систем линейных уравнений. Часто вы встретите ссылки на правило Крамера, симплекс-метод или симплексную таблицу. Эти методы сложнее, чем методы, описанные в этой главе. Существует множество применений матричной алгебры в бизнесе и науке, мы же затронули ее настолько, насколько необходимо для наших целей. Для более подробного изучения матричной алгебры и ее применений в бизнесе и науке рекомендую прочитать книгу «Множества, матрицы и линейное программирование» Роберта Л. Чилдресса (Sets, Matrices, and Linear Programming, by Robert L. Childress). Следующая глава посвящена методам, уже рассмотренным в этой главе, применительно к любому торгуемому инструменту с использованием оптимального f и механических систем.
Читать дальшеИнтервал:
Закладка:










