РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров

что можно представить следующим образом:

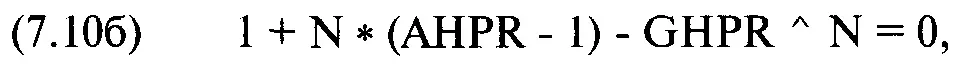
или

или

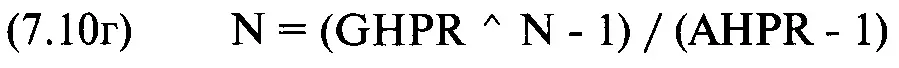
N в уравнениях с (7.10а) по (7. 10г) представляет собой количество сделок, кото­рое необходимо для того, чтобы геометрическое HPR стало равно арифметичес­кому. Все три уравнения эквивалентны. Решение можно получить методом ите­раций. Зная для нашего геометрического оптимального портфеля GHPR= 1,01542 и соответствующее AHPR= 1,031 и решая любое уравнение с (7.10а) по (7. 10г), мы находим, что N = 83,49894. Таким образом, после того, как пройдет 83,49894 сделки, геометрическое TWR догонит арифметическое. Полу­ченный результат справедлив для тех TWR, которые соответствуют координате дисперсии геометрического оптимального портфеля.Так же, как и AHPR, GHPR имеет свою линию CML. Рисунок 7-5 показывает как AHPR, так и GHPR с линиями CML, рассчитанными на основе безрисковой ставки.

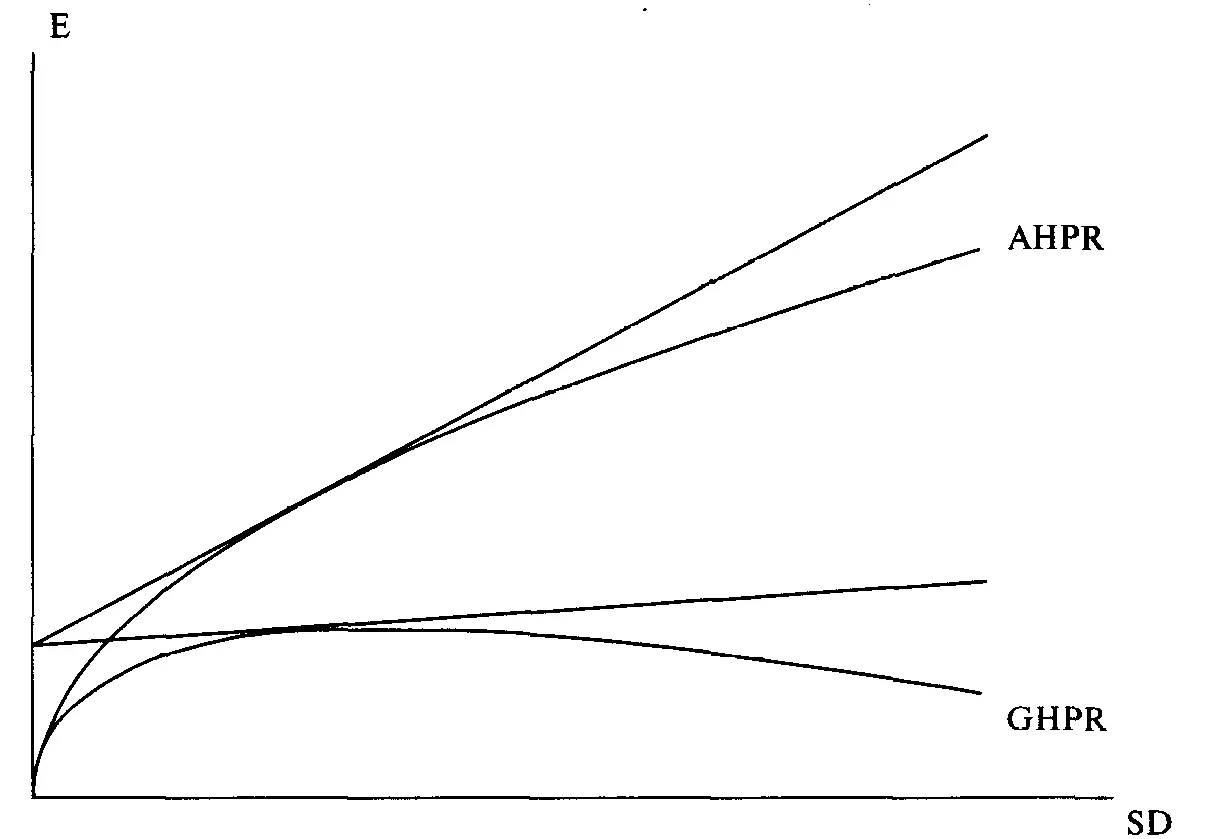
Рисунок7-5 AHPR, GHPR и их линии CML

Зная CML для AHPR, можно рассчитать CML для GHPR следующим образом:

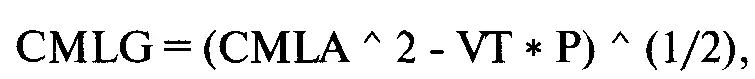
CMLG = координата Е (по вертикали) линии CML для GHPR при данной координате V, соответствующей Р;

CMLA= координата Е (по вертикали) линии CML для AHPR при данной координате V, соответствующей Р;

Р = процент в касательном портфеле, рассчитанный из (7.02);

VT = координата дисперсии касательного портфеля.

Следует иметь в виду, что для данной безрисковой ставки касательный портфель и геометрический оптимальный портфель в общем случае не одинаковы. Портфели будут идентичными при выполнении следующего равенства:

(7.12) RFR=GHPROPT-1,

где RFR = безрисковая ставка;

GHPROPT = среднее геометрическое HPR геометрического оптималь­ного портфеля, т.е. координата Е портфеля на эффектив­ной границе.

Только когда разность GHPR геометрического оптимального портфеля и еди­ницы равна безрисковой ставке, геометрический оптимальный портфель и ка­сательный портфель будут одинаковыми. Если RFR > GHPROPT - 1, тогда гео­метрический оптимальный портфель будет слева (т.е. иметь меньшую диспер­сию, чем касательный портфель). Если RFR < GHPROPT - 1, тогда касательный портфель будет слева (т.е. иметь меньшую дисперсию, чем геометрический оп­тимальный портфель). Во всех случаях касательный портфель, конечно же, ни­когда не будет иметь более высокое GHPR, чем геометрический оптимальный портфель.

Отметьте также, что точки касания CML к GHPR и CML к AHPR имеют одну координату SD. Мы можем использовать уравнение (7.01а) для поиска касатель­ного портфеля GHPR, заменив в (7.01а) AHPR на GHPR. В результате получится следующее уравнение:

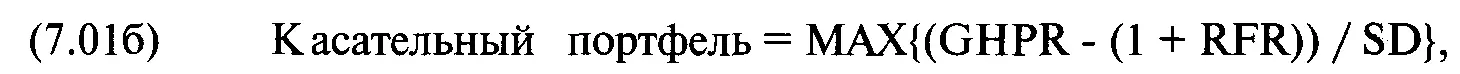
где МАХ{}= максимальное значение;

GHPR = геометрическое среднее HPR, т.е. координата Е данного портфеля на эффективной границе;

SD = стандартное отклонение HPR, т.е. координата SD данного портфеля на эффективной границе;

RFR = безрисковая ставка.

Неограниченные портфели

В этом разделе мы увидим, что можно поднять прибыли выше линии GCML, если снять ограничение на сумму весов. Давайте вернемся к геометрическим оп­тимальным портфелям. Если мы попробуем составить геометрический опти­мальный портфель из наших четырех рыночных систем — Toxico, Incubeast, LA Garb и сберегательного счета, то с помощью уравнений с (7.0ба) по (7.06г) най­дем, что он является таковым при Е, равном 0,1688965, и V, равном 0,1688965. Среднее геометрическое такого портфеля будет равно 1,094268, а состав портфе­ля будет иметь вид:

Toxico 18,89891%

Incubeast 19,50386%

LA Garb 58,58387%

Сберегательный счет 0,03014%

При решении уравнений с (7.06а) по (7.06г) необходимо использовать метод ите­раций, т.е. выбирать тестируемое значение для Е и решать матрицу для этого Е. Если полученное значение дисперсии больше значения Е, это означает, что тес­тируемое значение Е слишком высокое и в следующей попытке следует его пони­зить. Вы можете определить дисперсию портфеля, используя одно из уравнений с (6.06а) по (6.06г). Повторяйте процесс, пока не будет выполняться любое из ра­венств с (7.06а) по (7.06г). Таким образом вы получите геометрический оптималь­ный портфель (отметьте, что все рассмотренные портфели на эффективной гра­нице AHPR или на эффективной границе GHPR определяются с учетом того, что сумма весов равна 100%, или 1,00). Вспомните уравнение (6.10), используемое в первоначальной расширенной матрице для поиска оптимальных весов портфеля, уравнение отражает тот факт, что сумма весов равна 1:

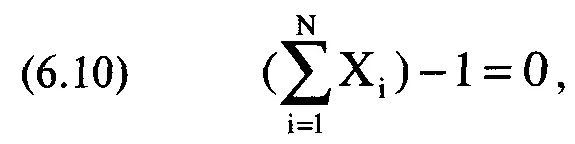
где N = количество ценных бумаг, составляющих портфель;

X. = процентный вес ценной бумаги L Уравнение также можно представить следующим образом:

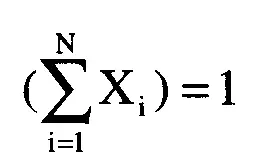
Мы можем найти неограниченный оптимальный портфель, если левую часть этого уравнения приравнять к числу больше 1. Для этого добавим еще одну рыночную систему, называемую беспроцентным вкладом (non-interest-bearing cash (NIC)), в первоначальную расширенную матрицу Данная рыночная система будет иметь дневное среднее арифметическое HPR= 1,0, а стандартное отклонение, диспер­сию и ковариацию дневных HPR равными 0. Коэффициенты корреляции NIC с любой другой рыночной системой всегда равны 0.

Теперь установим ограничение суммы весов на некоторое произвольное чис­ло, большее единицы. Хорошим первоначальным значением будет количество используемых рыночных систем (без NIC), умноженное на три. Так как мы имеем 4 рыночные системы (не учитывая NIC), то ограничим сумму весов 4*3=12.

Отметьте, что мы просто устанавливаем ограничение на произвольное значе­ние, большее единицы. Разность между этим выбранным значением и суммой полученных весов будет весом системы NIC.

На самом деле, мы не собираемся инвестировать в NIC. Это просто дополни­тельная переменная, с помощью которой мы создадим матрицу для получения

неограниченных весов рыночных систем. Теперь возьмем параметры наших че­тырех рыночных систем из главы 6 и добавим NIC: