РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров
- Название:Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров
- Автор:
- Жанр:
- Издательство:Альпина Паблишер
- Год:2007
- ISBN:ISBN 978-5-9614-0610-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров краткое содержание
Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
(7.02) P=SX/ST,
где SX = координата стандартного отклонения определенной точки на линии CML;
ST = координата стандартного отклонения касательного портфеля;
Р= процент активов, которые необходимо инвестировать в касательный портфель, чтобы быть на линии CML для данного значения SX.
Таким образом, если значение стандартного отклонения точки на линии CML (0,08296) из последней строки таблицы разделить на значение стандартного отклонения касательного портфеля (0,02986), мы получим 2,7782, что соответствует 277,82%.
В последнем столбце таблицы показано AHPR линии CML при данной координате стандартного отклонения. Оно рассчитывается следующим образом:
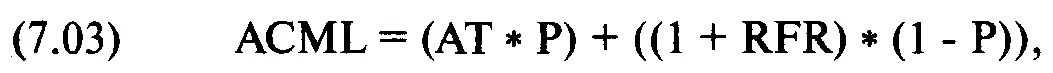
где ACML = AHPR линии CML при данной координате риска, или соответствующем проценте, рассчитанном из (7.02);
AT =значение AHPR касательной точки, полученное из (7.01а);
Р= процент в касательном портфеле, рассчитанный из (7.02);
RFR= безрисковая ставка.
Стандартное отклонение определенной точки на линии CML для данного AHPR рассчитывается следующим образом:
(7.04) SD=P*ST,
где SD = стандартное отклонение в данной точке на линии CML при определенном проценте Р, соответствующем данному AHPR;
Р = процент в касательном портфеле, рассчитанный из (7.02);
ST = значение стандартного отклонения касательного портфеля.
Геометрическая эффективная граница
Особенность рисунка 7-1 состоит в том, что он отображает арифметическое среднее HPR. Если прибыли реинвестируются, то для координаты эффективной границы по оси Y правильнее рассматривать геометрическое среднее HPR. Такой
подход многое меняет. Формула для преобразования точки на эффективной границе из арифметического HPR в геометрическое такова:
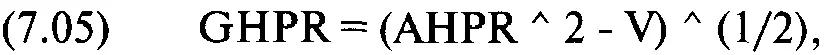
где GHPR = геометрическое среднее HPR;
AHPR = арифметическое среднее HPR;
V= координата дисперсии (она равна координате стандартного отклонения в квадрате).
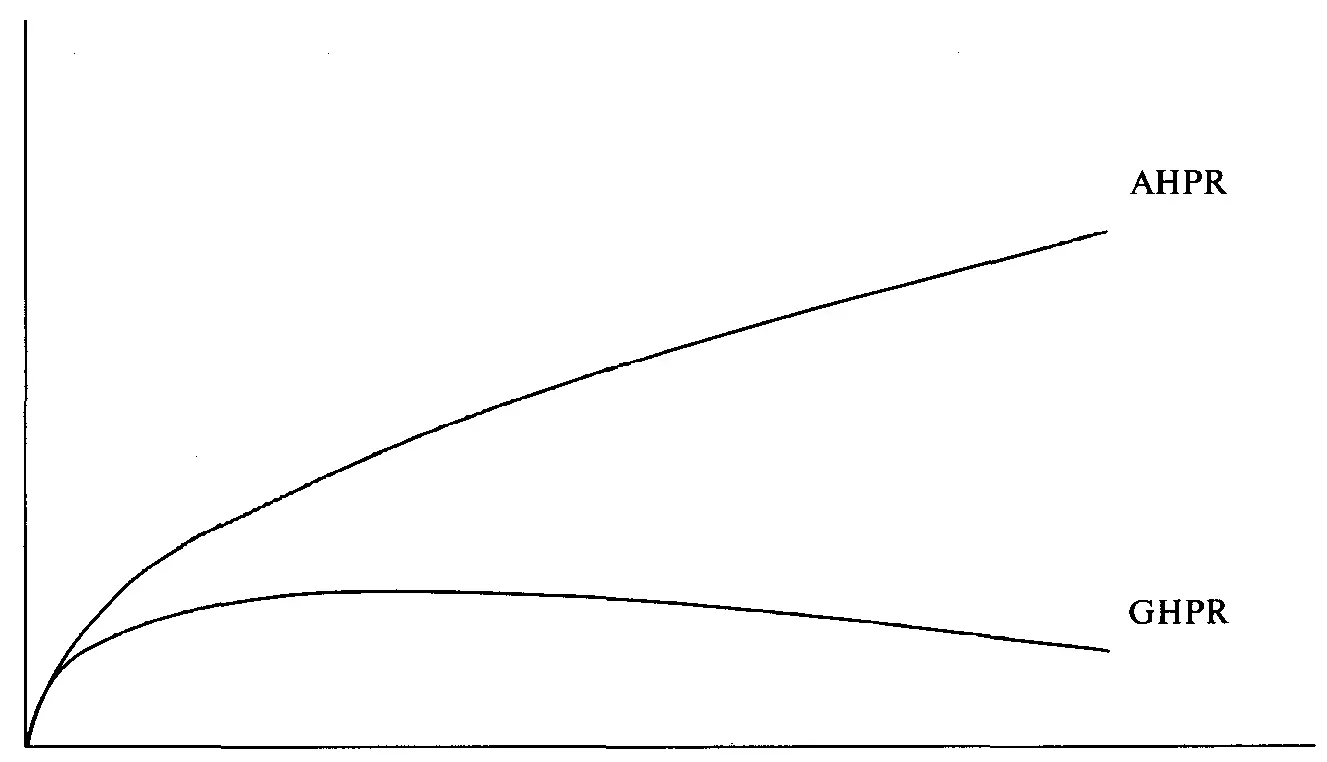
Рисунок7-2 Эффективная граница с реинвестированием и без реинвестирования
На рисунке 7-2 показана эффективная граница, соответствующая арифметическим средним HPR, и граница, соответствующая геометрическим средним HPR. Посмотрите, что происходит с эффективной границей при реинвестировании.
Построив линию GHPR, можно определить, какой портфель является геометрически оптимальным (наивысшая точка на линии GHPR). Вы можете найти этот портфель, преобразовав AHPR и V каждого портфеля на эффективной границе AHPR в GHPR с помощью уравнения (7.05) и выбрав максимальное значение GHPR. Однако, зная AHPR и V портфелей, лежащих на эффективной границе AHPR, можно еще проще определить геометрический оптимальный портфель, он должен удовлетворять следующему уравнению:
(7.06a) AHPR-1-V=0,
где АН PR = арифметическое среднее HPR, т.е. координата Е данного портфеля на эффективной границе;
V= дисперсия HPR, т.е. координата V данного портфеля на эффективной границе. Она равна стандартному отклонению в квадрате.
Уравнение (7.06a) также можно представить следующим образом:
(7.06б) AHPR - 1 = V
(7.06в) AHPR-V=1
(7.06г) AHPR=V+1
Необходимо сделать небольшое замечание по геометрическому оптимальному портфелю. Дисперсия в портфеле в общем случае имеет положительную корреляцию с наихудшим проигрышем. Более высокая дисперсия обычно соответствует портфелю с более высоким возможным проигрышем. Так как геометрический оптимальный портфель является портфелем, для которого Е и V равны (при E=AHPR- 1), мы можем допустить, что геометрический оптимальный портфель будет иметь высокие проигрыши. Фактически, чем больше GHPR геометрического оптимального портфеля (т.е. чем больше зарабатывает портфель), тем больше может быть его текущий проигрыш (откат по балансу счета), так как GHPR положительно коррелирован с AHPR. Здесь мы видим некий парадокс. С одной стороны нам следует использовать геометрический оптимальный портфель, с другой — чем выше среднее геометрическое портфеля, тем большими будут откаты по балансу счета в процентном выражении. Мы знаем также, что при диверсификации следует выбирать портфель с наивысшим средним геометрическим, а не с минимальным проигрышем, но эти величины стремятся в противоположных направлениях! Геометрический оптимальный портфель — это портфель, который расположен в точке, где линия, прочерченная из (0, 0) с наклоном 1, пересекает эффективную границу AHPR.
Рисунок 7-2 показывает эффективные границы на основе одной сделки. Мы можем преобразовать геометрическое среднее HPR в TWR с помощью уравнения:
(7.07) GTWR = GHPR^ N,
где GTWR = значение вертикальной оси, соответствующее данному GHPR после N сделок;
N - число сделок, которые мы хотим использовать.
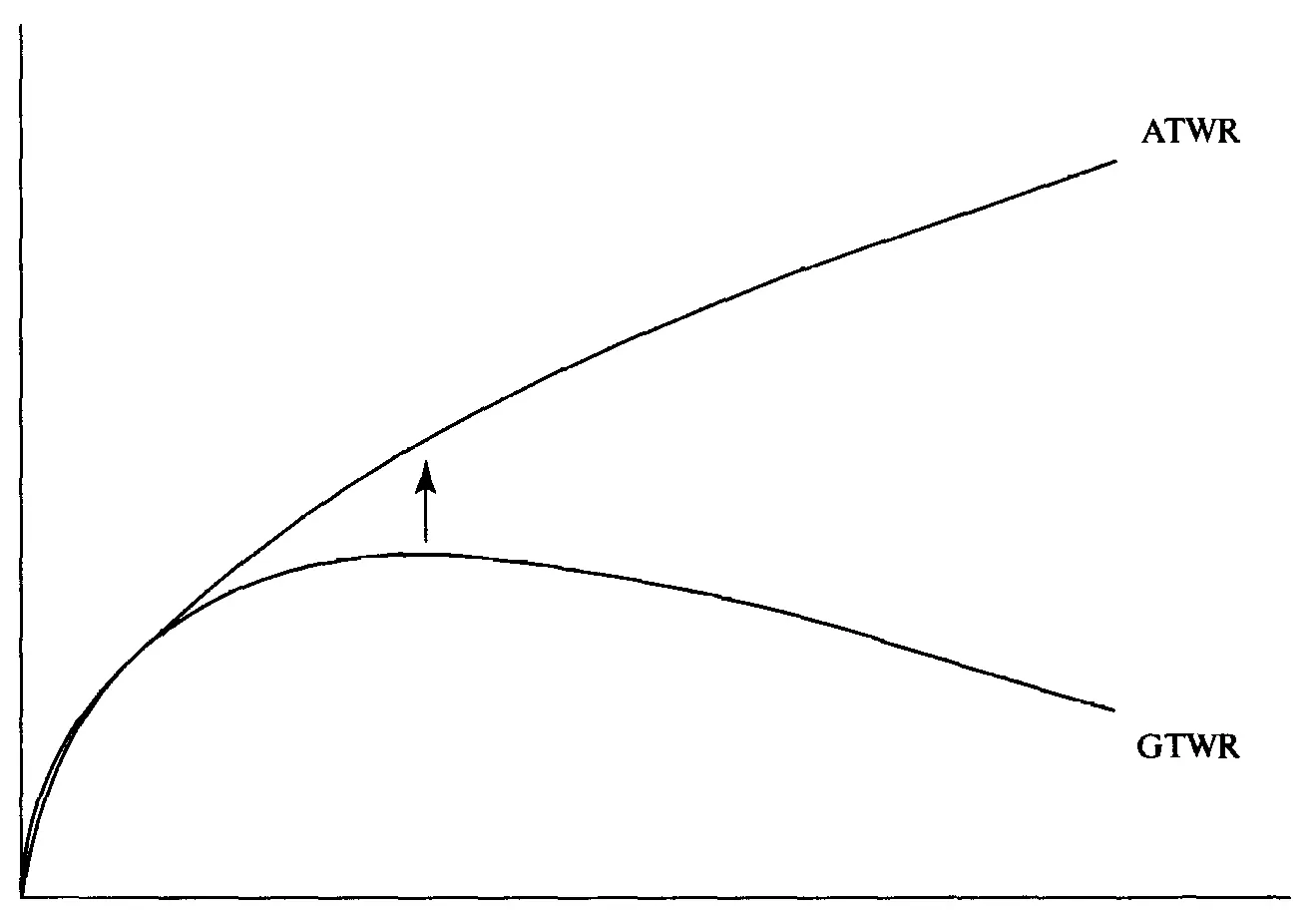
Рисунок7-3 Эффективная граница с реинвестированием и без реинвестирования
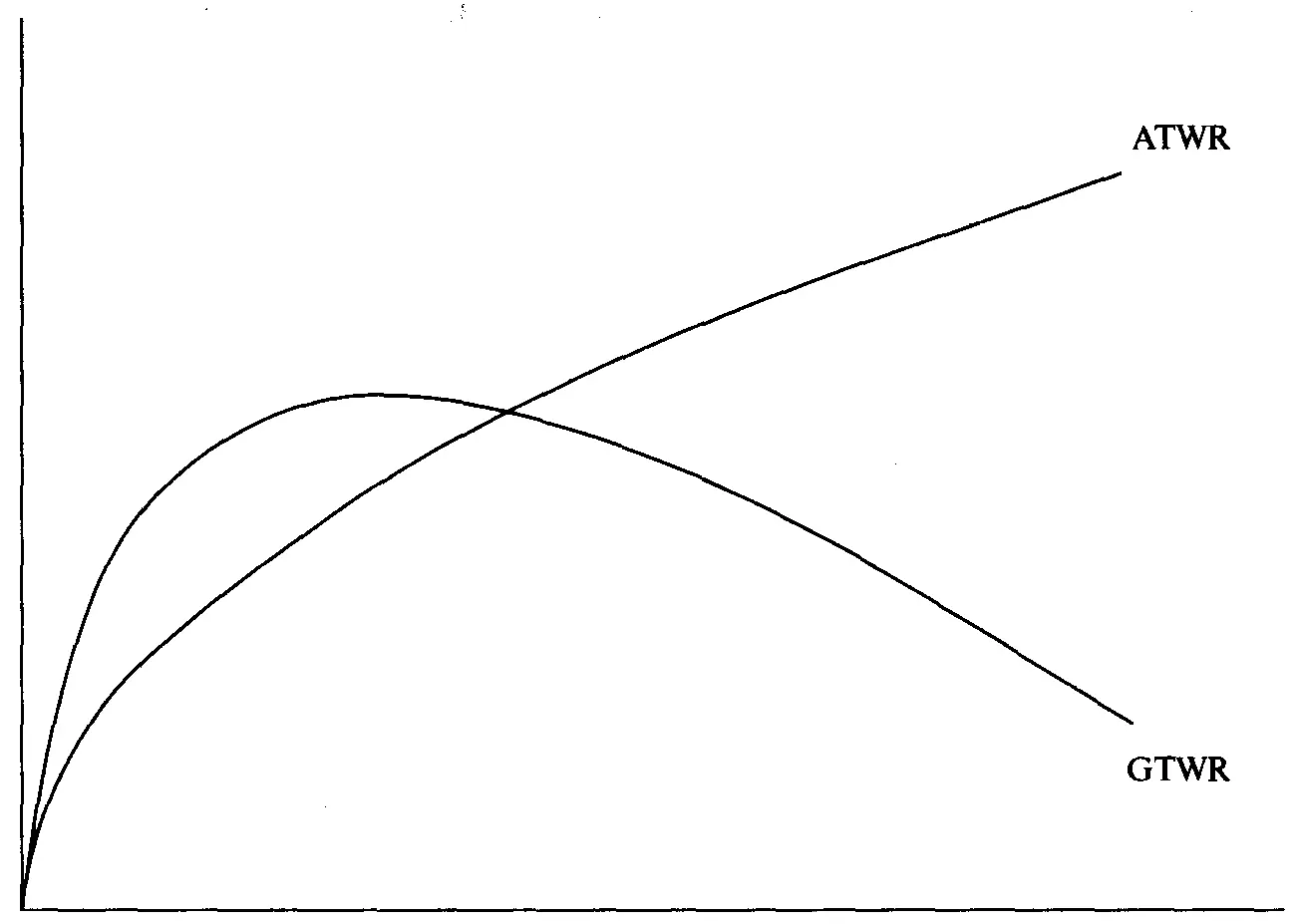
Рисунок7-4 Эффективная граница с реинвестированием и без реинвестирования
Пусть нашей целью будет AHPR при значении V, которое соответствует геометрическому оптимальному портфелю. В знаменателе (2.09а) мы используем среднее геометрическое геометрического оптимального портфеля. Теперь мы можем определить, сколько сделок необходимо для того, чтобы привести наш геометрический оптимальный портфель к одной сделке арифметического портфеля:
N=ln(l,031)/ln(l,01542) =0,035294/0,0153023 = 1,995075
Таким образом, можно ожидать, что через 1,995075, или приблизительно через 2 сделки, оптимальное GHPR достигнет соответствующего (при том же V) AHPR для одной сделки. Здесь возникает проблема, которая заключается в том, что ATWR должно отражать тот факт, что прошли две сделки. Другими словами, когда GTWR приближается к ATWR, ATWR двигается вверх, хотя и с постоянной скоростью (в отличие от GTWR, которое ускоряется). Можно решить эту проблему с помощью уравнений (7.07) и (7.08) для расчета геометрического и арифметического TWR:
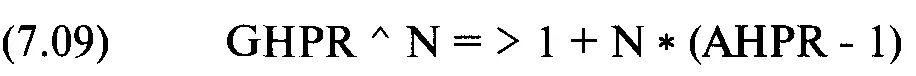
Так как мы знаем, что, когда N = 1, G всегда меньше А, можно перефразировать вопрос: «При скольких N G будет равно А?» Математически это будет выглядеть таким образом:
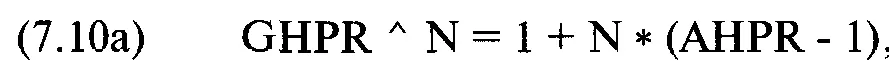
Интервал:
Закладка:










