РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров
- Название:Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров
- Автор:
- Жанр:
- Издательство:Альпина Паблишер
- Год:2007
- ISBN:ISBN 978-5-9614-0610-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров краткое содержание
Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
| Число стандартных отклонений | |||||
| 2 | 3 | 5 | 8 | 10 | |
| AHPR | 1,000102 | 1,000379 | 1,000409 | 1,000409 | 1,000409 |
| GHPR | 1,000047 | 1,00018 | 1,000195 | 1,000195 | 1,000195 |
| f | 0,043989 | 0,0781 | 0,0806 | 0,0806 | 0,0806 |
| Дата выхода | 911105 | 911105 | 911106 | 911106 | 911106 |
AHPR и GHPR — это арифметические и геометрические HPR при оптимальном f для дня закрытия 911105 (самая благоприятная дата выхода, так как она имеет наивысшие AHPR и GHPR). f соответствует оптимальному f для 911105. Значения строки «Дата выхода» — это последние даты, когда еще существует положительное ожидание (т.е. когда AHPR и GHPR больше 1). Интересно отметить, что AHPR, GHPR, f и Дата выхода сходятся к определенным значениям, когда мы увеличиваем число стандартных отклонений. За пределами 5 стандартных отклонений эти значения едва заметно изменяются, за пределами 8 стандартных отклонений они практически вообще не изменяются. Недостатком использования большого числа стандартных отклонений является необходимость в значительном компьютерном времени. В нашем примере это не так важно, но когда мы будем рассматривать одновременную торговлю по нескольким позициям, вы увидите, что каждая дополнительная позиция экспоненциально увеличивает необходимое компьютерное время. Для одной позиции 8 стандартных отклонений более чем достаточно, однако для нескольких позиций, открытых одновременно, необходимо уменьшить число стандартных отклонений. Следует отметить, что правило 8 стандартных отклонений применимо только тогда, когда логарифмы изменений цены распределены нормально.
Одиночная короткая позиция по опциону
Все сказанное по поводу одиночной длинной опционной позиции остается верным и для одиночной короткой опционной позиции. Единственное отличие заключается в ином написании уравнения (5.14):
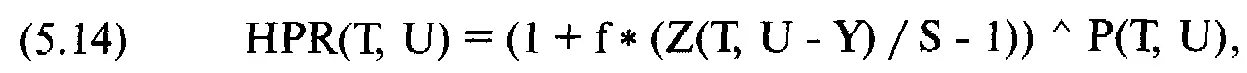
где HPR(T, U) = НРR для данного тестируемого значения Т и U;
f = тестируемое значение f;
S = текущая цена опциона;
Z(T, U - Y) = теоретическая цена опциона, когда цена базового инструмента равна U - Y, а время, оставшееся до срока истечения, равно Т,
Р(Т, U) = вероятность того, что базовый инструмент равен U, когда время, оставшееся до истечения срока исполнения, равно Т;
Y = разность между арифметическим математическим ожиданием базового инструмента (согласно уравнению (5.10)) и текущей ценой.
Для одиночной короткой опционной позиции это уравнение преобразуется в:
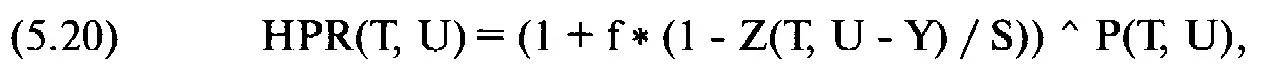
где HPR(T, U) == HPR для данного тестируемого значения Т и U;
f= тестируемое значение f;
S = текущая цена опциона;
Z(T, U - Y)= теоретическая цена опциона, когда цена базового инструмента равна U - Y, а время, оставшееся до срока истечения, равно Т;
Р(Т, U) = вероятность того, что базовый инструмент равен U, когда время, оставшееся до истечения срока исполнения,
равно Т,
Y = разность между арифметическим математическим ожиданием базового инструмента (согласно уравнению (5.10)) и текущей ценой.
Обратите внимание, что единственным отличием уравнения (5.14) для одиночной длинной опционной позиции от уравнения (5.20) для одиночной короткой позиции является выражение (Z(T, U-Y)/S-1), которое заменяется на (1-Z(T, U - Y) / S). Все остальное в отношении одиночной длинной опционной позиции верно и для одиночной опционной короткой позиции.
Одиночная позиция по базовому инструменту
В главе 3 мы подробно рассмотрели математику поиска оптимального f параметрическим способом. Теперь мы можем использовать тот же метод и для
одиночной длинной опционной позиции с учетом нового HPR, которое рассчитывается по уравнению (3.30):
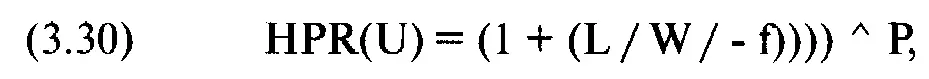
где HPR(U) = HPR для данного U;
L= ассоциированное P&L;
W = ассоциированное P&L худшего случая (это всегда отрицательное значение);
f == тестируемое значение f;
Р = ассоциированная вероятность.
Для длинной позиции переменная L, т.е. ассоциированное P&L, определяется как разность между ценой базового инструмента U и ценой S.
(5.21 а) L для длинной позиции = U - S
Для короткой позиции ассоциированное P&L рассчитывается наоборот:
(5.216) L для короткой позиции = S - U,
где S = текущая цена базового инструмента;
U = цена базового инструмента для данного HPR.
Мы можем также рассчитать оптимальное f для одиночной позиции по базовому инструменту, используя уравнение (5.14). При этом надо иметь в виду, что оптимальное f может получиться больше 1.
Пусть цена базового инструмента равна 100, и мы ожидаем пять результатов:
| Результат | Вероятность | P&L |
| 110 | 0,15 | 10 |
| 105 | 0,30 | 5 |
| 100 | 0,50 | 0 |
| 95 | 0,25 | -5 |
| 90 | 0,10 | -10 |
Отметьте, что исходя из уравнения (5.10) наше арифметическое математическое ожидание по базовому инструменту составляет 100,576923077. Это означает, что переменная Y для (5.14) равна 0,576923077, так как 100,576923077-100= = 0,576923077. Если рассчитать оптимальное f, используя столбец P&L и уравнение (3.30), мы получим f= 1,9, что соответствует 1 единице на каждые 52,63 доллара на счете. Если в уравнении (5.14) использовать данные из столбца «Результат», тогда переменная S равна 100. В этом случае мы не вычитаем значение Y (арифметическое математическое ожидание базового инструмента минус его текущая цена) из U при определении переменной Z(T, U - Y), и получаем оптимальное f около 1,9, что соответствует 1 единице на каждые 52,63 доллара на счете, так как
100 /1,9=52,63.
Если вычесть значение Y в выражении Z(T, U - Y), являющемся элементом уравнения (5.14), мы получим математическое ожидание по базовому инструменту, равное его текущему значению, и поэтому f не будет оптимальным. Тем не менее нам следует вычесть значение Y в Z(T, U - Y) для того, чтобы соответствовать расчетам цен опционов, а также формуле «пут-колл» паритета. Если мы будем использовать уравнение (3.30) вместо уравнения (5.14), тогда из каждого значения U в (5.21а) и (5.216) следует вычесть значение Y, то есть надо вычесть Y из каждого P&L, что опять же создает ситуацию, когда нет положительного математического ожидания, и поэтому нет оптимального значения f. Все вышесказанное означает, что если мы откроем позицию по базовому инструменту, не имея никаких представлений о направлении движения его цены, то не получим положительного математического ожидания (как происходит с некоторыми опционами) и поэтому не найдем оптимального f. Мы можем получить оптимальное f только в том случае, когда математическое ожидание положительное. Это произойдет, если базовый инструмент «в тренде».
Читать дальшеИнтервал:
Закладка:










