РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров

Р(Т, U) = 1-хвостая вероятность того, что цена базового инстру­мента равна U, когда время, оставшееся до истечения срока исполнения, равно Т. Это значение можно опре­делить из любой формы распределения, которую пользователь посчитает подходящей;

Y = разность между арифметическим математическим ожиданием базового инструмента (согласно уравнению (5.10)) и текущей ценой.

Необходимо отметить, что форма распределения, используемого для Р(Т, U), не обязательно должна быть такой же, как и в модели ценообразования, применяе­мой для определения значений Z(T, U - Y). Например, вы используете модель фондовых опционов Блэка-Шоулса для определения значений Z(T, U - Y). Эта модель предполагает логарифмически нормальное распределение изменений цены, однако для определения соответствующего Р(Т, U) вы можете использовать другую форму распределения.

Шаг7. Теперь мы можем начать поиск оптимального f с помощью метода итераций, перебирая все возможные значения f между 0 и 1, или с по­мощью метода параболической интерполяции, или любого другого одномерного алгоритма поиска. Подставляя тестируемые значения f в HPR (у вас уже есть HPR для каждого из возможных приращений цены между + 3 и - 3 стандартными отклонениями на дату истечения срока или указанную дату выхода), вы можете найти среднее геомет­рическое для данного тестируемого значения f. Для этого надо пере­множить все HPR, и полученное произведение возвести в степень единицы, деленной на сумма вероятностей:

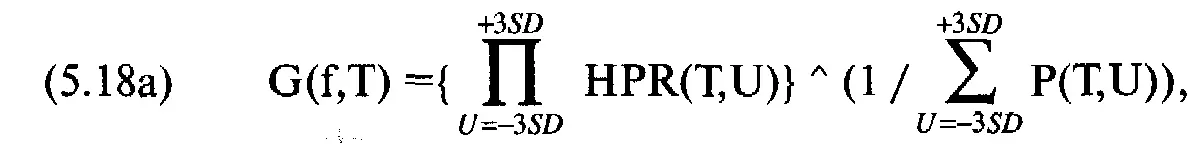
поэтому

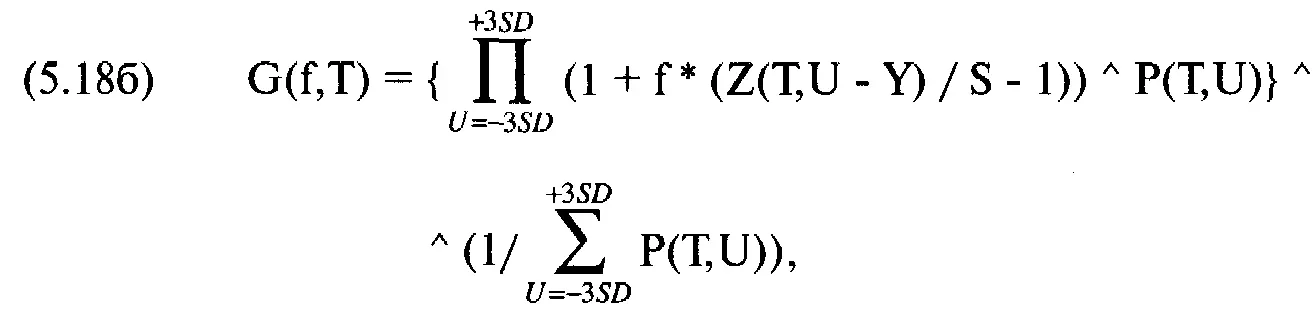
где G(f, T) = среднее геометрическое HPR для данного тестируемого зна­чения f;

f = тестируемое значение f;

S = текущая цена опциона;

Z(T, U - Y) = теоретическая цена опциона, когда цена базового инстру­мента равна U - Y, а время, оставшееся до срока истечения, равно Т. Эту цену можно определить с помощью любой мо­дели ценообразования, которую пользователь посчитает подходящей;

Р(Т, U) = вероятность того, что базовый инструмент равен U, когда вре­мя, оставшееся до истечения срока исполнения, равно Т. Это значение можно определить из любой формы распределения, которую пользователь посчитает подходящей;

Y = разность между арифметическим математическим ожидани­ем базового инструмента (согласно уравнению (5.10)) и теку­щей ценой.

Значение f, которое в результате даст наибольшее среднее геометрическое, явля­ется оптимальным.

Мы можем оптимизировать f, определив оптимальную дату выхода. Другими словами, мы можем найти значение оптимального f для данного опциона на каж­дый день между текущим днем и днем истечения. Запишем оптимальные f и сред­ние геометрические для каждой указанной даты выхода. Когда мы завершим эту процедуру, мы сможем найти ту дату выхода, которая даст наивысшее среднее гео­метрическое. Таким образом, мы получим день, когда должны выйти из позиции по опциону для того, чтобы математическое ожидание было наивысшим (т.е. среднее геометрическое было наивысшим). Мы также узнаем, какое оптимальное количество контрактов следует купить.

Теперь у нас есть математический метод, с помощью которого можно выхо­дить из позиции по опциону и покупать опцион при положительном математи­ческом ожидании. Если мы выйдем из позиции в день, когда среднее геометри­ческое максимально и оно больше 1,0, то следует покупать число контрактов, исходя из оптимального f, которое соответствует наивысшему среднему геомет­рическому. Математическое ожидание, о котором мы говорим, — это геометри­ческое ожидание. Другими словами, среднее геометрическое (минус 1,0) являет­ся математическим ожиданием, когда вы реинвестируете прибыли (арифмети­ческое положительное математическое ожидание будет, конечно же, выше, чем геометрическое).

После того как вы найдете оптимальное f для данного опциона, можно преобра­зовать полученное значение в число контрактов, которое следует покупать:

(5.19) K=INT(E/(S/f)),

где К = оптимальное число опционных контрактов для покупки;

f= значение оптимального Г(от 0 до 1);

S = текущая цена опциона;

Е = общий баланс счета;

1NT() = функция целой части.

Для расчета TWR следует знать, сколько раз мы хотели бы воспроизвести эту же сделку в будущем. Другими словами, если наше среднее геометрическое составля­ет 1,001 и необходимо найти TWR, которое соответствует этой же игре 100 раз подряд, то TWR будет 1,001^100 = 1,105115698. Поэтому можно ожидать за­работка в 10,5115698%, если провести эту сделку 100 раз. Формула для преобразо­вания среднего геометрического в TWR задается уравнением (4.18):

(4.18) TWR = Среднее геометрическое ^ X,

где TWR = относительный конечный капитал;

Х = число раз, которое мы «повторяем» эту игру.

Мы можем определить и другие побочные продукты, например, геометрическое математическое ожидание (среднее геометрическое минус 1). Если мы возьмем наибольший возможный проигрыш (стоимость самого опциона), разделим его на оптимальное f и умножим на геометрическое математическое ожидание, то полу­чим среднюю геометрическую сделку. Как вы уже заметили, при использовании метода оптимального f в торговле опционами появляется еще один побочный продукт — оптимальная дата выхода. Мы рассматривали позиции по опционам при отсутствии направленного движения цены базового инструмента. Для указанной даты выхода точки, сме­щенные на 3 стандартных отклонения выше и ниже, рассчитываются из теку­щей цены, таким образом, мы ничего не знаем о будущем направлении цены базового инструмента. В соответствии с математическими моделями ценообразования мы не получим положительное арифметическое математическое ожи­дание, если будем удерживать позицию по опциону до срока истечения. Одна­ко, как мы уже видели, можно достичь положительного геометрического мате­матического ожидания, если закрыть позицию в определенный день до срока истечения.

Если вы предполагаете определенное изменение цены базового инструмен­та, его можно учесть. Допустим, мы рассматриваем опционы на базовый инст­румент, который в настоящее время стоит 100. Далее предположим, что на ос­нове анализа рынка выявлен тренд, который предполагает цену 105 к дате исте­чения, и эта дата отстоит на 40 рыночных дней от сегодняшней даты. Мы ожидаем, что цена повысится на 5 пунктов за 40 дней. Если исходить из линей­ного изменения цены, то цена должна расти в среднем на 0,125 пунктов в день. Поэтому для завтрашнего дня (как дня выхода) мы возьмем значение U, равное 100,125. Для следующей даты выхода возьмем U, равное 100,25. К тому време­ни, когда указанная дата выхода станет датой истечения срока опциона, U бу­дет равно 105. Если базовым инструментом является акция, то вы должны вы­честь дивиденды из U, воспользовавшись уравнением (5.04). Тренд можно учи­тывать, если изменять каждый день значение U, исходя из сделанного прогноза. Так как уравнения (5.17а) и (5.176) изменятся, значения U повлияют на оптимальные f и побочные продукты. Отметьте, что в уравнениях (5.17а) и (5.176) используются новые значения U, т.е. происходит автоматическое при­ведение данных, следовательно, полученные оптимальные f будут основаны на данных, приведенных к текущей цене.