Кит Йейтс - Математика жизни и смерти. 7 математических принципов, формирующих нашу жизнь

Разницу в подходах к этому сюжету и, соответственно, разницу в политических повестках каждого из трех новостных агентств, обнаружить несложно. В речи людей явно отражаются их партийно-политические пристрастия. А вот манипуляции с цифрами менее заметны. Статистику можно подобрать так, чтобы представить определенный взгляд на вещи – и сохранить при этом видимость объективности. Противоречащие выводу цифры просто игнорируются, и за счет выборочного использования данных искажается реальность. Иногда ненадежными оказываются сами исследования. Небольшие, нерепрезентативные или предвзятые выборки в сочетании с наводящими вопросами и выборочным представлением данных – вот рецепт недостоверного статистического исследования. Есть еще более тонкий прием – использовать статистику вне контекста: 300-процентный рост заболеваемости может означать и увеличение количества заболевших с одного пациента до четырех, и с 500 тысяч человек до двух миллионов. Контекст важен. Подвох не в том, что каждая иная интерпретация чисел является ложью сама по себе – напротив, каждая из них представляет собой маленький кусочек правдивой истории, которую кто-то представил в предпочтительном для него свете. Подвох в том, что это не вся правда. Нам остается попытаться собрать воедино истинную историю, стоящую за журналистскими перегибами.

В этой главе мы проанализируем и развенчаем уловки, ловушки и махинации в газетных заголовках, рекламных объявлениях и политической риторике. Более того, мы увидим, что схожие математические манипуляции применяются и там, где им вовсе не место, – при консультировании пациентов и даже в научных статьях. Мы представим простые способы распознать, когда от нас утаивают часть информации. Мы познакомимся с инструментами, которые помогут вскрыть манипуляции со статистикой. И в конце концов выясним, когда мы должны верить «правде».

Самыми незаметными и часто эффективными математическими трюками являются те, в которых участие чисел даже не просматривается. Заявив, что «даты имеют особенное значение для исламских боевиков», Горка косвенно предложил читателям оценить шанс того, что два теракта пришлись на одну и ту же дату случайно, дав понять, что сам он считает это очень маловероятным. Реальный же ответ можно выяснить, проведя математический мысленный эксперимент под названием «парадокс дней рождения».

Этот парадокс формулируется так: «Сколько нужно людей, чтобы вероятность того, что хотя бы у двоих из них день рождения придется на одну дату, превысит 50 %?» Обычно, впервые столкнувшись с этим вопросом, люди останавливаются на числе 180, что примерно в два раза меньше количества дней в году. Дело в том, что в такой ситуации мы склонны прикидывать вероятность того, что дата рождения кого-то из «присутствующих» совпадет с нашей. Но 180 – это много. Слишком много. С учетом обоснованного предположения, что дни рождения распределены по дням года примерно равномерно, верный ответ – всего 23 человека. Фокус в том, что нас интересует не сама дата, на которую выпадает день рождения, а только возможные совпадения.

Чтобы понять, почему нужно так мало народа, для начала стоит подсчитать количество пар, которые образуются в комнате, – ведь мы ищем именно пару людей, у которых совпадает день и месяц рождения. Чтобы вычислить, сколько пар могут образовать 23 человека, представьте себе, что все они выстроились в ряд и начали по очереди пожимать друг другу руки. Первый человек пожмет руку 22 другим, второй – 21 человеку (с первым он уже это сделал), третий – 20 и так далее. Наконец, предпоследний человек пожимает руку последнему, а нам остается сложить 22 + 21 + 20 +… + 1. Для 23 человек это относительно просто, но когда людей в комнате будет больше 50, это станет уже несколько более утомительным. Такие суммы – последовательных целых чисел, начиная с единицы, – называются треугольными числами, поскольку их можно представить в виде упорядоченного треугольного массива, как мы это сделали на рис. 15. К счастью, для треугольных чисел есть простая и красивая формула. Для общего числа людей N в комнате число рукопожатий составит N×(N-1)/2. Для 23 человек это дает 23×22/2, или 253 пары. Когда пар так много, вероятность, что, хотя бы у одной из них дата рождения будет совпадать, составит больше 50 % – и это, пожалуй, уже не вызывает удивления.

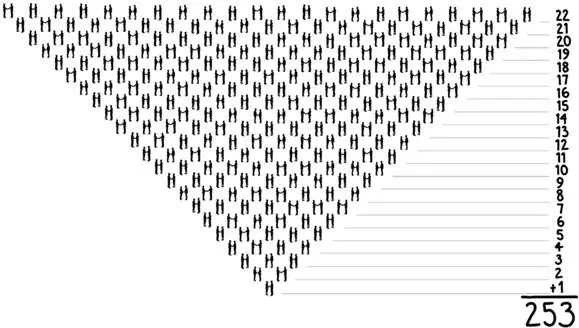
Рис. 15. Количество рукопожатий между 23 людьми. Первый человек пожимает руку 22 другим, второй – 21, и так до тех пор, пока предпоследний не останется один на один с последним человеком, которому он еще не пожимал руку. Общее количество рукопожатий между 23 людьми – это сумма первых 22 целых чисел. Формула для треугольных чисел говорит, что 23 человека могут составить 253 пары

Для проверки проще сначала просчитать вероятность, что дни рождения у всех будут разными. Мы уже использовали такую методику во второй главе, когда вычисляли, сколько маммографий может пройти женщина до того, как вероятность получить ложноположительный диагноз составит более 50 %. У каждой отдельной пары определить вероятность несовпадения дат рождения легко. Первый человек может отмечать свой день рождения в любой из 365 дней в году, а второй – в любой из оставшихся 364 дней. Таким образом, вероятность, что у одной пары людей дата рождения не совпадает, близка к абсолютной и составляет 364/365 (или 99,73 %). Однако поскольку пар всего 253, нам нужно вычислить вероятность того, что ни в одной из оставшихся 252 пар даты рождения тоже не совпадают. Если бы все эти пары были независимы друг от друга, то вероятность несовпадения даты рождения была бы равна результату перемножения вероятности несовпадения даты рождения у одной пары (364/365) на саму себя еще 252 раза, то есть (364/365) 253. Хотя результат деления 364 на 365 достаточно близок к единице, при столь многократном перемножении этого числа на себя вероятность, что ни у одной из пар дни рождения не будет совпадать, оказывается 0,4995, что чуть меньше 1/2. Поскольку в нашем случае есть только два вероятных исхода: даты рождения не совпадают ни у одной из пар или даты рождения совпадают у двух или более человек (математики называют такие связанные варианты исчерпывающим множеством), сумма вероятностей этих двух событий должна составлять единицу. Таким образом, вероятность, что у двух или более человек даты рождения совпадают, составляет 0,5005, то есть чуть более 1/2.

В реальности не все пары дней рождения будут независимы друг от друга. Если у человека A дата рождения совпадает с датой рождения человека B, а у того – с датой рождения человека C, то даты рождения в паре A – C тоже совпадают, и, следовательно, не являются независимыми. Если бы они были независимыми, то шанс иметь общую дату рождения у них составлял бы только 1/365. Точный расчет вероятности совпадения с учетом этих зависимостей лишь немногим сложнее, чем при независимых величинах в предыдущем абзаце. При таком расчете мы добавляем людей «в комнату» по одному. Как мы уже установили, для двух человек вероятность несовпадения даты рождения составляет 364/365. Когда к ним добавляется третий, дата рождения каждого из трех может приходиться на любой из оставшихся 363 дней в году (если у кого-то не обнаружится общая дата рождения с кем-то из оставшейся пары). Таким образом, вероятность того, что у трех человек не совпадут даты рождения, составляет (364/365) × (363/365). Четвертому достается уже только 362 дня, поэтому вероятность, что даты рождения не совпадут у четверых, несколько снижается – до (364/365) × (363/365) × (362/365). Этот ряд продолжается до тех пор, пока к вечеринке не присоединится последний, 23-й участник. Его день рождения может выпасть на любой из оставшихся 343 дней. Вероятность того, что ни у кого из 23 человек даты рождения не совпадут, определяется последовательным перемножением: