Кит Йейтс - Математика жизни и смерти. 7 математических принципов, формирующих нашу жизнь

С 2009 по 2013 год компания L’Oreal рекламировала и продавала линейку «омолаживающих» продуктов Lancome Genifique. Наряду с обычной псевдонаучной чепухой («Молодость в ваших генах. Реактивируйте ее», «Повысьте активность генов и стимулируйте выработку протеинов молодости») рекламные материалы демонстрировали гистограмму, утверждавшую, что всего после семи дней использования этого средства кожа 85 % потребителей приобрела «идеальное сияние», у 82 % – стала «удивительно гладкой», у 91 % – «мягкой, как перышко», а 82 % отметили «общее улучшение вида кожи». Если не обращать внимание на безнадежно расплывчатые описания, то эти цифры звучат чрезвычайно впечатляюще, уверенно подтверждая качество продукта.

Но стоит повнимательнее присмотреться к цифрам, и мы увидим совершенно другую историю. Женщин, принявших участие в исследовании, просили применять Genifique дважды в день, а затем высказать свое отношение к утверждениям вроде: «кожа выглядит более сияющей», «цвет кожи выглядит более ровным» или «кожа по ощущениям стала более мягкой». Степень согласия с подобными утверждениями их просили оценить по девятибалльной шкале – от «полностью не согласна» (единица) до «полностью согласна» (девятка). Их не просили оценить степень сияния, мягкости или гладкости их кожи; они оценивали только степень своего согласия (или несогласия) с тем, что улучшение вообще есть. И уж, конечно, их не просили добавлять к оценкам эпитеты вроде «идеально» или «удивительно».

Результаты опроса показали, что, хотя 82 % женщин согласились (выставив оценку от шести до девяти баллов по девятибалльной шкале), что их кожа выглядит более гладко через семь дней, «полностью согласились» с этим менее 30 %. Точно так же 85 % в целом были согласны с тем, что их кожа выглядит более сияющей, но только 35,5 % согласились с этим полностью. L’Oreal подретушировала результаты собственного исследования, чтобы они выглядели более впечатляющими, чем на самом деле.

Размер фокус-группы – компания опросила всего 34 женщины – вызывал, пожалуй, еще бóльшие сомнения. При таком небольшом количестве участников в достоверности результатов опроса трудно быть уверенным из-за так называемого отклонения малой выборки. Малые размеры выборки, как правило, показывают более существенные отклонения от истинного среднего значения по популяции, чем большие выборки. Проиллюстрируем это мысленным экспериментом с «правильной монетой», на которой строго в половине случаев выпадает орел, в половине – решка. По какой-то причине я хочу убедить окружающих, что монета «предвзята» в пользу решки. Допустим, что для этого достаточно, чтобы монета выпадала решкой по крайней мере в 75 % случаев. Как будут меняться мои шансы убедить их по мере того, как увеличивается размер выборки – количество подбрасываний монеты?

Я могу попытаться обойтись всего одним броском. Если выпадет решка, я буду счастлив; одна решка в одном броске – это больше, чем пороговые 75 %. Такое возможно в половине случаев. Наилучший мой шанс убедить окружающих в своей правоте – сделать всего один бросок, но они могут справедливо возразить, что им требуется больше данных, чтобы быть уверенными, и попросят меня подбросить монету еще раз. При двух бросках мне нужно, чтобы решка выпала дважды – если решка и орел выпадут по разу, вероятность выпадения будет равна только 50 % и мои аргументы не пройдут. Как видно на рис. 17, две решки – это только один из четырех равновероятных результатов при двух бросках правильной монеты, так что я сумею убедить только четверть зрителей. Вероятность того, что монета выпадет решкой по крайней мере в 75 % бросков, быстро уменьшается по мере увеличения размера выборки, как показано на рис. 18. Когда размер выборки дойдет до ста бросков, мои шансы убедить кого-либо в том, что монета «предвзята», упадут до 0,00000009.

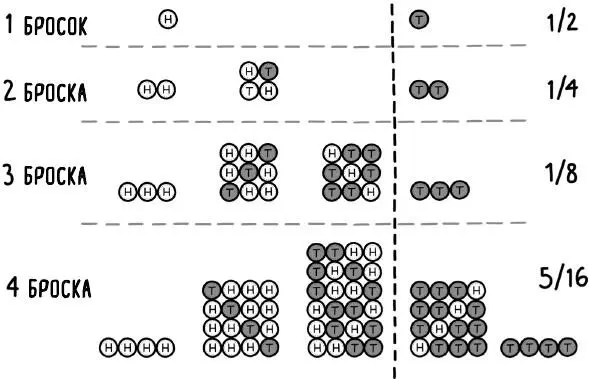
Рис. 17. Возможные комбинации орлов (H) и решек (T), выпадающие при различном количестве бросков монеты, до четырех бросков включительно. Справа от разделительной линии показаны результаты, когда решки выпадают по крайней мере в 75 % случаях, слева – когда они выпадают реже

По мере увеличения размера выборки уменьшается разброс вокруг среднего значения (в данном случае средним значением будет 50 % решек); становится все труднее убедить кого-то в том, что это неправда. Поэтому достоверность представленных в рекламе L’Oreal результатов, которые были получены на выборке всего 34 человека, не может не вызывать определенные сомнения.

Как правило, рекламные объявления, основанные на результатах «исследований» с небольшой выборки, сообщают о своих достижениях в процентах (82 % имеют удивительно гладкую кожу), а не в сравнительных долях (кожа стала удивительно гладкой у 28 из 34 участников), чтобы скрыть досадно малый размер выборки. При этом совпадение хотя бы двух показателей (как и в рекламе Genifique, где два показателя были одинаковыми: «удивительную гладкость» и «общее улучшение» отметили по 82 % участников) недвусмысленно свидетельствует о ее скромной величине. Более того, у маленькой выборки респондентов и выбор ответов невелик, если производитель хочет убедить потенциальных покупателей, что товар хорош, но опасается переборщить с его расхваливанием (позитивные оценки в диапазоне от 95 до 100 % могут выглядеть подозрительно). При большом размере выборки вероятность того, что на два разных вопрос в одинаково положительные ответы даст равное количество людей, гораздо меньше.

Рис. 18. Чем чаще мы подбрасываем настоящую «правильную монету», тем быстрее тают шансы убедить кого-то в том, что она «предвзята» в пользу решки

В 2014 году Федеральная торговая комиссия (ФТК) направила компании L’Oreal предупреждение об использовании недостоверной информации в рекламе линейки продуктов Genifique [113] Ramirez, E., Brill, J., Ohlhausen, M. K., Wright, J. D., Terrell, M., & Clark, D. S. (2014). In the matter of L’Oreal USA, Inc., a corporation. Docket No. C. Retrieved from https://www.ftc.gov/system/files/documents/cases/140627lorealcmpt.pdf . ФТК утверждала, что цифры на диаграммах объявлений были «ложными или вводящими в заблуждение» и не подтверждены научными исследованиями. В ответ L’Oreal согласилась прекратить «заявления об этих продуктах, искажающие результаты любых тестов или исследований».

Достоверность исследования продуктов линейки Genifique, по всей видимости, была скомпрометирована не только отклонением малой выборки, но и такими погрешностями отбора, как умышленные ошибки в ответах или пристрастный выбор респондентов. Если L’Oreal набирала участников исследования, например, через объявление на своем сайте, то на это объявление, скорее всего, отреагировали женщины, изначально благосклонно настроенные к продуктам L’Oreal и готовые высоко их оценить (умышленные ошибки в ответах). Или же компания намеренно выбирала для участия в тесте тех женщин, кто и раньше давал хорошие отзывы о продуктах L’Oreal (пристрастный выбор респондентов).