Кит Йейтс - Математика жизни и смерти. 7 математических принципов, формирующих нашу жизнь

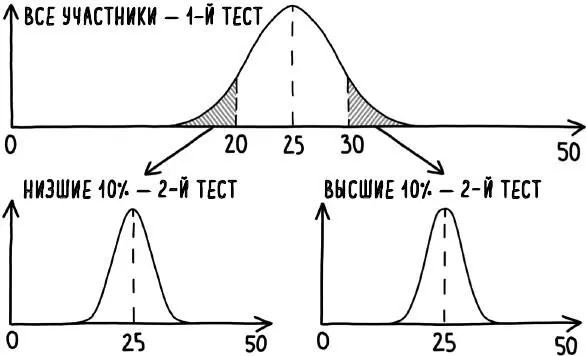
Рис. 20. Распределение баллов при прохождении теста из 50 вопросов с многовариантными ответами «да/нет». При повторном тестировании тех, кто набрал наивысшие 10 % баллов (заштрихованная область справа), их средний балл совпадает со средним общим баллом. То же самое относится к низшим 10 % (заштрихованная область слева). Группы, получившие как высшие, так и низшие баллы, регрессировали в сторону среднего значения

Результат реальных экзаменов в значительной степени будет определяться навыками и трудовой этикой, однако нельзя исключать и элемент везения, который проявляется как в наборе вопросов, выпадающих на экзамене, так и в приоритетности предметов для повторного экзамена. Регрессия к среднему способна выявить такой эффект – если он имел место. Элемент случайности особенно заметен на экзаменах с многовариантным набором ответов, из которых даже студент, не обладающий необходимыми знаниями, может угадать правильный. В одном исследовании, проведенном в 1987 году, 25 подверженных «экзаменационной панике» американских студентов, которые неожиданно плохо справились с тестом на проверку академических способностей (SAT), прошли повторное тестирование, предварительно приняв пропранолол – лекарство от гипертонии [134] Faigel, H. C. (1991). The effect of beta blockade on stress-induced cognitive dysfunction in adolescents. Clinical Pediatrics, 30 (7), 441–5. https://doi.org/10.1177/000992289103000706 . Газета New York Times сообщала о результатах исследования так: «Препарат, используемый для лечения высокого кровяного давления, резко улучшил результаты теста на проверку академических способностей у студентов, страдающих от необычайно сильной тревожности…». Студенты, принимавшие пропранолол, значительно повысили свои оценки – в среднем на 130 баллов по шкале от 400 до 1600. Поначалу кажется, что пропранолол – невероятно действенное средство. Оказывается, однако, что даже ученики, которые не нервничали перед тестом, при повторной сдаче улучшают свои оценки примерно на 40 баллов. Если учесть, что студенты, отобранные для исследования, были выбраны именно потому, что они показали результаты хуже, чем предполагалось по их IQ или другим академическим показателям, они вполне могли бы и без пропранолола значительно повысить свои баллы в результате регрессии к среднему.

Без контрольной группы студентов, получивших такие же низкие баллы на первом тесте и прошедших переэкзаменовку без препарата, эффект его воздействия определить нельзя. Очень соблазнительно было бы приписать прогресс студентов воздействию пропранолола, основываясь только на результатах получавшей его группы. Однако итоги случайного теста с многовариантными ответами показывают, что регрессия групп, показавших экстремальные результаты, к среднему значению является чисто статистическим феноменом.

В медицинских исследованиях очень важно не путать причину со следствием (не говоря уже о подтасовке причинно-следственных связей). Один из способов предотвратить это (как мы уже видели в главах 2 и 3) – рандомизированное контролируемое исследование, в котором пациенты распределяются случайным образом по двум группам. Как и в исследовании тамоксифена (средства от рака груди), пациенты в группе лечения получают настоящую терапию, а пациенты в контрольной группе – плацебо. Если и пациенты, и организаторы не знают, в какой из групп находится конкретный пациент, исследование называют двойным слепым. Это считается золотым стандартом клинических испытаний. При двойном слепом рандомизированном контролируемом исследовании любая разница между улучшением в контрольной группе и улучшением в группе лечения может быть надежно отнесена исключительно на счет лечения, исключая регрессию к среднему.

Исторически любое улучшение пациентов в контрольной группе исследования привыкли называть эффектом плацебо – ощущением пользы от терапии, которую испытуемый считает лечением, даже если это всего лишь таблетка-пустышка. Однако становится все более очевидным, что он складывается из двух совершенно разных явлений. Первое – подлинный психосоматический эффект, который заставляет пациентов чувствовать себя лучше только потому, что они верят в факт лечения. Этот эффект истинного плацебо реально изменяет оценку пациентом своих симптомов – до некоторой степени. Психосоматический эффект усиливается, если пациент знает, что его лечат по-настоящему, и, что интересно, он усиливается, даже если об этом знает только тот, кто проводит лечение, – отсюда и необходимость двойного слепого исследования. Впрочем, психосоматический аспект, по всей видимости, оказывает наименьшее влияние на формирование и интенсивность эффекта плацебо.

Вторая, возможно, более значимая причина улучшения состояния пациентов в контрольной группе, – регрессия к среднему. Этот простой статистический эффект не приносит никакой пользы пациентам вообще. Единственный способ определить, какой из двух компонентов эффекта плацебо оказывает наибольшее воздействие, – сравнить результаты «лечения» в контрольных группах с результатами группы, которая не получает лечения вообще. Эти виды испытаний часто считают неэтичными, но в прошлом их провели достаточно много, чтобы показать, что большинство эффектов плацебо на самом деле являются результатом регрессии к среднему [135] Hrobjartsson, A., & Gotzsche, P. C. (2010). Placebo interventions for all clinical conditions. Cochrane Database of Systematic Reviews, (1). https://doi.org/10.1002/14651858.CD003974.pub3 .

Многие сторонники альтернативной медицины утверждают, что даже если их лечение является не более чем эффектом плацебо, польза от него может быть значительной и стоит того. Тем не менее, если бóльшая часть эффекта плацебо вызвана регрессией к среднему, который не дает никакой реальной пользы для пациента, этот аргумент неубедителен. Другие гуру альтернативной медицины утверждают, что ставку нужно делать не на «искусственные клинические испытания», а на «реальные результаты» – иными словами, на «неконтролируемые результаты испытаний, которые фиксируют только то, как меняется состояние пациента после лечения». Неудивительно, что шарлатаны цепляются за любой аргумент, который позволяет им выдавать последствия регрессии к среднему за благоприятный эффект их знахарства. Лауреат Пулитцеровской премии Эптон Синклер сказал: «Трудно заставить человека понять хоть что-то, когда его зарплата зависит от его непонимания».

Эффект регрессии к среднему оказывает сильнейшее влияние на интерпретацию причинно-следственных связей не только в медицине, но и в законотворчестве. 16 октября 1991 года 32-летняя Сюзанна Гратиа Хапп зашла со своими родителями в кафе в техасском городке Киллин. В обеденное время кафе было забито – за квадратными столиками теснились полторы сотни голодных клиентов. В 12:39 лишившийся работы моряк торгового судна Джордж Хеннард протаранил своим голубым пикапом Ford Ranger витрину кафе и въехал прямо в обеденную зону. Выпрыгнув с водительского места с пистолетами Glock 17 и Ruger P89, он открыл стрельбу [136] Событие известно, как «Резня в «Луби»». – Прим. ред. .