Николай Болотов - Парадоксы интеллектуального чтива. Книга четвёртая «Сказ про то, что есть Прописная Истина»

В ход идут мощные компьютеры. Процессор x86 при попытке выполнить операцию целочисленного деления на ноль формирует особый случай, вектор которого также находится по адресу 0.

В результате процессор славное действие деления на ноль до конца не доводит, а перескакивает в другое место, обычно сообщая о внезапном отказе.

Ведь процесс деления целых чисел осуществляется компьютером, как вычитание со сдвигом и обнулением остатка от делимого. При этом нулевой делитель означает бесконечное число циклов с одинаковым ненулевым результатом. В результате делимое списывается в остаток и возвращается нуль.

Бесконечности не получается……..

Здесь компьютер возвращает нас к древним основам арифметики. Вспомним, что человечество придумало арифметические действия умножения и деления, специально изобретя таблицу умножения, и только для того, чтобы быстрее прибавить или отнять части физического сомножества объектов, без занудного перекладывания пар их из кучи в кучу. То есть в основе этих действий лежат сложение и вычитание, что, кстати, нам подтверждает компьютер, не имеющий понятия об ухищрениях произведения и частного. Он все себе быстренько складывает или вычитает, по принципу есть объект, нет объекта.

Поэтому примитивные арифметические действия с физическими объектами в сфере ноля – Ничто и – Континуум – физически абсурдны. Что очевидно на примере деления на ноль в образной житейской (физической) логике…10 яблок делим на 2.

Скажем, мать раздаёт 10 яблок двум своим детям поровну, и у каждого в руках оказывается по 5 штук.

При делении на 1 = все яблоки достаются одному.

А при «делении на ноль», при физическом отсутствии деления, когда никто никому яблок не раздаёт? Яблоки должны остаться на месте, нетронутыми, тем более не превращаться в бесконечное множество плодов.

Ноль и бесконечность суть атрибуты Космоса и, покуда мы не познаем его физическую сущность, никакая цифирь нам тут не поможет. А особо изощренная, только навредит, произвольно создавая абстрактных монстров мироздания. Вся теория относительности – типичный результат такого произвола.

Космогония этой теории в своей абсурдности могла прийти только в больную голову физика или в абстрактную – математика: « Вселенная создается скоростью фотонов света, в до того, абсолютной Пустоте Космоса».

Куда долетели они, там есть пространство Вселенной, которая «конечна, но безгранична»!? Ну, а куда не долетели – там всё та же Пустота. И если Вселенная после взрыва «схлопнется» в цифру ноль, Вселенная исчезнет и возвратиться опять Пустота, в которой, глядишь, опять что-то взорвется…….А как не взорвётся!?

Ничего неделанье, также, как и ничего не понимание, в физическом мире ничего не изменяет. И бомбардировка первозданной материи Космоса формулами высшей математики напоминает мне действо циркового клоуна.

Очевидно, что в физике мироздания нет ничего более сложного, чем алгоритм есть – нет, с постепенным увеличением или уменьшения количества, при диалектическом переходе количества в качество и наоборот…….

Ну, вот, после такого многоречивого вступления мы переходим к неформальному рассмотрению математического множества Кантора. Кантор имел в виду просто нескончаемую прямую линию, которую можно без конца делить на всё более и более мелкие отрезки. Мы же её мыслим, как физическую величину: пространства или энергии.

И то что пространство возможно представить в виде неограниченной по протяжённости прямой, следует из простой логики: окружность, имеющая радиус длиной в бесконечность, должна трансформироваться в бесконечную прямую. В этом случае сфера может быть изображена в виде куба беспредельного объёма.

Я это всё к тому, чтобы как-то представить себе на месте математической прямой некий физический объект, изменяющийся по определённым правилам.

Итак, перед нами схема получения Канторового множества.

Первая линия – это теоретический размер Континуума.

Поделим его на три равные части. Средний отрезок выкинем. Останется два отрезка суммарной длины 2/3. С каждым из них проделаем точно такую же операцию. Останется четыре отрезка суммарной длины 4/9.

Продолжая так далее, до бесконечности, получаем множество, которое имеет меру меньше любой наперёд заданной положительной величины, то есть меру ноль. Но это ноль с точки зрения математики, которая может измываться над этими отрезками бесконечно, доказывая мощность множества, счетность, плотность и так далее….

В точности уподобляясь спору схоластов на тему: – Сколько чертей уместится на кончике иглы?

Логика процесса, очевидно, говорит нам, что вести его в сторону уменьшения можно бесконечно долго, чтобы получить нечто близкое к точке для первоначально бесконечного пространства или что-либо безэнергетическое для энергетики Вселенной. Также совершенно очевидно, что противоположный процесс ведет к преобразованиям материи от уровня Ничто к уровню Континуума – бесконечности.

Следуя этой логике, мы не станем идти вслед за Кантором в математических премудростях числового ряда с его счислениями и несчислениями бесконечного нуля, то бишь к тем же схоластическим чертям.

Вместо этого воспользуемся рациональном зерном истины, добытой математикой в известном парадоксе Галилея: «Число цифр числового ряда всегда равно числу чётных чисел» (рис.13).

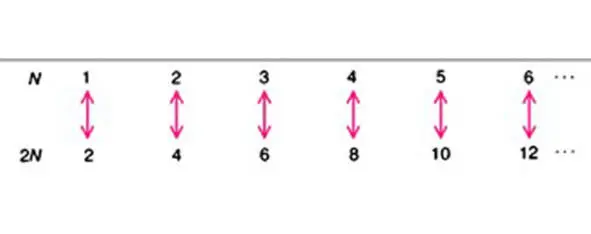
Таинства численного ряда (Рис.13)

Действительно, согласно рисунку слева, числовой парный ряд уходит в бесконечность. И целые числа его можно одно за другим объединить в пары с чётными числами, не исчерпав какого-либо из множеств этих чисел. В первой паре два числа рано четному – два, во второй – четыре цифры (1,2,3,4) дают четное число 4, в третьей 6=6 и т. д.

Фактически Кантор воспользовался Галилеевым парадоксом и превратил его в средство количественного сравнения бесконечных множеств.

Он назвал два множества эквивалентными, если между элементами этих множеств можно установить взаимно однозначное соответствие.

Предположим, что у нас имеется ведёрко, заполненное чёрными и цветными шариками. Каким образом можно сравнить количество чёрных и цветных шариков?…Простейший способ состоит в извлечении их из ведёрка парами, состоящими из чёрного и цветного шариков. Если каждый шарик может быть объединён в пару с шариком другого цвета, то два множества эквивалентны. Если нет, то оставшиеся в ведёрке шарики показывают, каких шариков было больше.

Кантор показал, что свойство, которое Галилей рассматривал, как парадоксальное, фактически является естественным свойством бесконечных множеств. Множество чётных чисел эквивалентно множеству всех целых положительных чисел, чётных и нечётных, вместе взятых. Для нас важно, что физически – это пары в бесконечности или парная модель волчков в Первовселенной!