Николай Болотов - Парадоксы интеллектуального чтива. Книга четвёртая «Сказ про то, что есть Прописная Истина»

В 1837 году В. Я. Струве обнаружил и измерил параллакс альфы Лиры. Полученное им значение (0,125» ± 0,055») было первым успешным определением параллакса звезды вообще. Это был первый шаг в осознании истинных пространственных масштабов Вселенной.

XX век – век рождения современной космологии.

Она рождается почти вровень с веком и по мере развития вбирает в себя все новейшие достижения, такие как технологии постройки больших телескопов, космические полёты и компьютеры.

В 1916 А. Эйнштейн пишет уравнения общей теории относительности – теории гравитации, ставшей основой для доминирующих космологических теорий. В 1917 году, пытаясь получить решение, описывающее «стационарную» Вселенную, Эйнштейн вводит в уравнения ОТО дополнительный параметр – космологическую постоянную. Но в последующем отказывается от идеи постоянства Вселенной.

В 1929 Эдвин Хаббл открывает закон пропорциональности между скоростью удаления галактик и расстоянием до них, позже названный его именем.

В 1932 году Ф. Цвикки выдвигает идею о существовании тёмной материи – вещества, не проявляющего себя электромагнитным излучением, но участвующего в гравитационном взаимодействии.

В 1946—1949 годах Г. Гамов, пытаясь объяснить происхождение химических элементов, применяет законы ядерной физики к началу расширения Вселенной. Так возникает теория «горячей Вселенной» – теория Большого Взрыва, а вместе с ней и гипотеза об изотропном реликтовом излучении с температурой в несколько градусов Кельвина.

В 1991—1993 годах в космических экспериментах «Реликт-1» и COBE открыты флуктуации реликтового излучения.

В 1998 году по далёким сверхновым звёздам типа Ia строится диаграмма Хаббла. Выясняется, что Вселенная расширяется с ускорением.

Итак, мы прошли, вернее, проскакали, весь путь Космологии от древности до современной теории происхождения нашей Вселенной в результате «Большого взрыва».

Сразу скажу, что ни в физическом, ни в философском смысле, эта теория меня не устраивает, поскольку в ней имеется масса абсурдного.

Но про критику как-нибудь потом, а сейчас давайте разберёмся, если уж ни что, ……то хоть как «бабахнуло» (Рис.11) ……

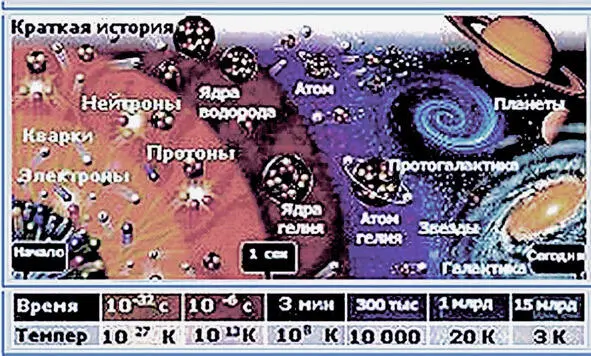
Современная «карта мира»

Современная релятивистская физика в целом оптимистично смотрит на катастрофу «большого взрыва», считая, что последние научные данные позволяют сделать вывод, что наша Вселенная действительно родилась 15 миллиардов лет назад в результате этого Большого взрыва. Что именно взорвалось в тот момент и что, собственно, существовало до Большого взрыва, этой наукой благоразумно откладывается на потом. Главное, слава богу таки взорвалось, а со взрывами физика оперирует с лёгкостью.

В общем, всё происходило, как на этой картинке. Что-то бабахнуло и творчески разлетелось, формируя Вселенную и, как положено взрывной волне постепенно охлаждаясь…….

Но такое статус-кво очевидно только в случае, если Большая Вселенная или Континуум представляет собой одновременно Всё и Ничто, или, в смысле математики, Бесконечность и Ноль. И хотя для абстрактной науки математики здесь никаких проблем не существует: она с лёгкостью оперирует этими понятиями, для современной физики здесь полный…..тупик.

Представить нечто бесконечное, переходящее в безразмерную точку, она не в силах. Она пытается, подражая математике, сотворить нечто физическое из математических догм через понятие «актуального нуля и актуальной бесконечности», но без философской логики тут не обходится.

Смотрим на одно из множества подобных начинаний:

« Подтвердить правильность этого предположения на сегодня можно, по-видимому, лишь на уровне общих законов диалектики. Например, закон перехода количественных изменений в качественные не выполнялся бы в полной мере, если бы не существовало качественно выделенных конечных величин, ограничивающих снизу и сверху множество значений той или иной физической величины.

На наш взгляд, идея о существовании актуальной бесконечности в актуальном нуле (и актуального нуля в актуальной бесконечности) заслуживает внимания, поскольку может явиться одним из фундаментальных методологических ориентиров (принципов) при разработке основ постклассической физики».

Мы тоже не лыком шиты и попытаемся внести свой вклад в разработку основ новой «постнеклассической физики». Но поскольку мы не гении от математики, то воспользуемся уже известными постулатами этой мудрой науки, придав математической абстракции некий физический, по возможности, смысл… Я имею в виду посылы, вытекающие из теории множества Кантора.

Посмотрим, что у нас получится.

Сразу оговоримся, что математика в этой гипотезе нас мало волнует. Нам нужна физика деления бесконечности на ноль.

Границу здесь провести почти невозможно, но великие математики её как-то интуитивно обнаруживали.

Так российский академик Леонард Эйлер ещё три века тому назад не уставал повторять, что при делении на ноль мы получаем бесконечное число, а не предел функции…….Он чётко разделил «нуль-число» и «нуль-предел», как совершенно различные, самостоятельные понятия.

Тем более что в математике считается, что поле действительных чисел является аддитивной группой (от лат. additio – прибавляю) – относящийся к сложению, а ноль – специфически нейтральный элемент этой группы. Поэтому помещая нейтральный ноль (пустое место) в эту группу, мы превращаем её во что-то группой не являющееся. Произвольно обращаться с нолем может только математика, считая его обычной цифрой.

Вот несколько абсурдов, взятых наугад….

Из правил умножения и деления известно, что при умножении число на ноль получается ноль, а при делении – бесконечность. Но такая формализация до добра не доводит……Действительно, пусть у нас есть два произвольных разных числа, a и b, и мы умеем делить на ноль. Далее – всё по элементарной алгебре:

0 * a = 0

0 * b = 0

0 * a = 0 * b

делим на 0, и формально, получается, по правилам алгебры

a = b

Таким же точно образом «доказывается», что 2+2=n. (где n=любое число) 0 = 0.

Всё также и в том же духе…….

(2+2) *0 = n*0

делим на 0, и получается

2+2 = n

Таков математический абсурд умножения на ноль.

Но при делении на ноль дело обстоит и того хуже. Все реальные попытки такового приводили к фантастическим парадоксам.

Для тех, кому на ноль делить все-таки очень уж хочется, в нестандартном анализе математики придумали гипердействительные числа так, например, существует число не равное нулю, но меньшее всех остальных по модулю.

Школьные знания здесь явно не помогают……..