Виктор Назаркин - Атмосфера должна быть чистой. Применение статистических методов при аттестации источников эмиссии и оценке качества атмосферного воздуха

Несмотря на то, что имеется официальный перечень показателей, характеризующих степень воздействия различных источников эмиссии ЗВ и показателей качества воздуха [3], в практике работы аналитических служб отсутствуют методики, которые позволили бы при организации работы системы контроля, получать из любых данных измерений концентрации, именно те характеристики, которые делают оценки степени загрязнения и санитарно-гигиенической обстановки наиболее объективными и однозначными [8, 9].

Для аттестации источников эмиссии и оценки качества воздуха в рабочей зоне предприятий или воздуха населенных мест эти характеристики должны быть различны, что вытекает из различия в «физическом» смысле имеющихся границ допуска ПДВ, (ПДС) или ПДК для радиоактивных и нерадиоактивных ЗВ. Вредное воздействие ЗВ в воздухе непосредственно связано со временем экспозиции.

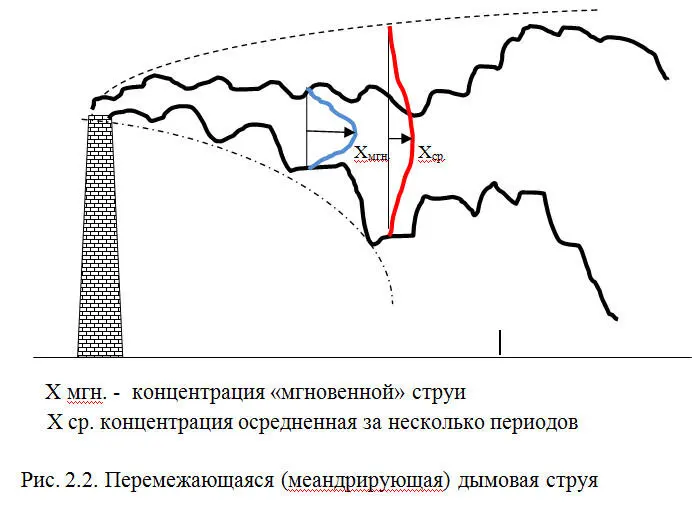
Измерения концентрации ЗВ в источниках выбросов и атмосферном воздухе показали, что результаты могут существенно зависеть от времени осреднения (времени отбора проб) [8 ]. Эта проблема имеет наибольшее значение для интерпретации данных измерений концентрации ЗВ в атмосферном воздухе и пылегазовых выбросах предприятий и не связана непосредственно с качеством использованной измерительной аппаратуры. Проблема связана непосредственно со случайным характером изменения во времени и пространстве гидрометеорологических параметров в точках наблюдения, а также комплекса технологических факторов. Однако проблема осреднения имеет место вообще при измерении и анализе любых, зависящих от времени случайных процессов [11]. Данные, полученные к настоящему времени показывают, что учет времени осреднения (времени отбора проб) – это чрезвычайно сложная операция. Например, если источник загрязнения атмосферы высокая труба, а загрязнения воздуха осуществляется под действием волнообразного дымового шлейфа (так называемая перемежающаяся или меандрирующая струя рис. 2.2.), то концентрация ЗВ может отсутствовать в один момент и достигать максимума 30 секунд спустя.

Таким образом, концентрация «мгновенной» струи Х мгн. будет давать больший максимум, чем осредненная за несколько периодов Х ср. На самом деле, в зависимости от метеоусловий и параметров источников может иметь место несколько разных типов дымовых струй [9]. Концентрации в порывах могут в 10 и более раз превышать средние значения, а длительность порывов может зависеть от расстояния до источника.

Средние значения концентрации за сутки, месяц или год легко могут оказаться близкими к 0,2, 0,05 или 0,01 от среднего значения, получаемого за час или три минуты, на которые могут оказать влияние факторы, локальные в пространстве и времени. В многочисленных работах, рассматривающих зависимость концентрации от времени осреднения, в том числе и на предприятиях ядерно-топливного цикла (ЯТЦ), указывается, что эта зависимость, полученная экспериментально для средних условий устойчивости атмосферы и периодов осреднения до нескольких часов может быть описана выражением:

Эта известная формула, полученная из статистической модели дымовой струи Гиффорда Ф.И. [ 18 ] для коррекции данных, полученных за разные периоды времени не может быть исчерпывающим решением проблемы.

Таким образом, соотношение (2.2) рекомендуется для прогнозных оценок, если можно экспериментальным, а не из расчета рассеяния, путем оценить и рассчитать концентрацию, осредненную за некоторый период времени. Для больших периодов осреднения вместо (2.2.) рекомендовано соотношение:

Если подобные формулы и дают представление о соотношениях между соответствующими величинами, то в силу локальных причин не позволяют оценить возможные экстремальные значения концентрации. Они не дают ни каких рекомендаций и алгоритмов при определении входящих в них величин, то есть по организации соответствующего контроля [8,9]. Единственная рекомендация, которая приводится в упомянутых работах, состоит в том, что любые данные нуждаются в коррекции и время отбора проб (время осреднения) всегда должно учитываться и приводиться вместе с данными о концентрациях.

Проблема осреднения по времени во многих случаях не учитывается при оценке санитарно-гигиенической обстановки из-за отсутствия соответствующих методических рекомендаций. Эта проблема не учитывается при сравнении работы приборов и методик определения концентрации отдельных ингредиентов ЗВ в источниках выбросов и объектах окружающей среды. Известно, что одним из возможных путей решения проблемы осреднения является реализация методик статистической фильтрации и гармонического анализа экспериментальных данных, что может позволить получить оценки экстремальных значений концентрации, соответствующих необходимым временам осреднения, однако для этого необходима детальная информация о процессе Х(t), чтобы избежать маскировки частот.

Метод гармонического анализа временных рядов состоит в представлении случайной функции в виде конечной суммы ряда Фурье, при этом случайная функция заменяется детерминированной, а для достижения достаточной точности (учета 95% реальной дисперсии) достаточно рассчитать 4 -5 членов разложения [ 11, 16 ].

Наиболее существенные результаты применения дисперсионного анализа можно ожидать при интерпретации данных о распределении концентрации ЗВ на больших территориях, то есть оценка изменчивости концентрации ингредиента по району, на котором расположены несколько стационарных постов контроля [19].

Одним из возможных способов оценки качества воздуха в приземном слое атмосферы на контролируемой территории является метод построения системы неслучайных ортогональных функций 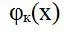таких, что отрезок ряда Фурье является наилучшей аппроксимацией случайной функции 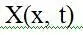в смысле средней квадратичной погрешности. Система функций 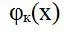такова, что приближенное равенство при определенном выборе коэффициентов 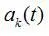описывает изменчивость поля концентрации 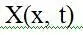лучше, чем линейная комбинация любых других функций, состоящая из такого же числа слагаемых.