Виктор Назаркин - Атмосфера должна быть чистой. Применение статистических методов при аттестации источников эмиссии и оценке качества атмосферного воздуха

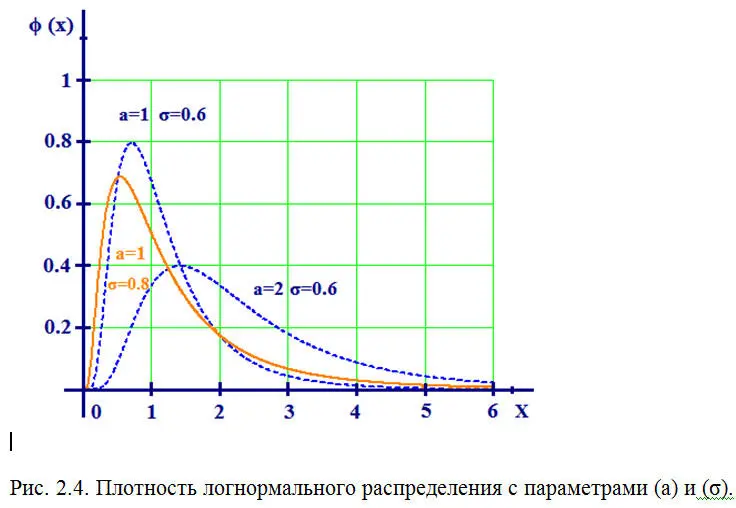
Правомерность использования распределения (2.15.) для аппроксимации распределения частот эмпирических данных о загрязнении воздуха и воды отмечалась во многих экспериментальных работах [22, 23, 29, 31,51], подобные выводы делались и из некоторых общих соображений [31], известны и попытки строгого математического доказательства этих факторов с использованием (распространением) центральной предельной теоремы на случай, когда отдельные измерения случайной величины (Х) не являются независимыми [ 5 ]. Аргументом в пользу применения логнормального распределения является его простая функциональная связь с распределением Гаусса, что позволяет использовать в готовом виде классические решения теории оценок и критериев значимости.

Использование функций от случайных величин вместо самих случайных величин может оказаться весьма плодотворным и в оценках параметров порядковых статистик [13, 14, 15]. Изучение вопроса о значениях порядковых статистик, играет принципиальную роль в возможности оценки экстремальных значений временных рядов. Смысл необходимости достоверных оценок экстремумов заключается в том, что основной задачей управления качеством окружающей среды является поддержание максимальных значений концентрации ЗВ ниже установленных границ допуска.

Стандарты качества воздуха качества воздуха характеризуются значениями предельно допустимых концентраций ПДК.

В других странах, например, США стандарты включают и другие интервалы осреднения – 1 час, 3 часа, 8 часов и некоторые другие. Из цитируемых работ можно заключить, что максимальная концентрация для каждого периода может быть превышена раз в году.

Формально данный вопрос можно исследовать с позиции теории пересечения некоторым случайным процессом Х(t) фиксированного уровня – границы допуска.

Теория проблем, связанных с пересечениями рассмотрена, например, в книге Крамера Г. и Лидбеттера М. [ 5 ].

Таким образом, следуя требованиям стандарта, значения функции Х(t) могут сколько угодно раз касаться уровня ПДК, но не должны пересекать его на всем интервале 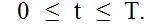. Однако, нужно иметь в виду, что если показанные на рис. 2.2. превышения 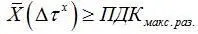, определенны за время 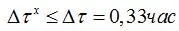, то эти превышения не правомерно рассматривать как нарушения стандарта качества воздуха.

Таким образом, четко определяется задача оценки санитарно-гигиенической обстановки. Это – оценка возможных экстремальных значений концентрации за отчетный период 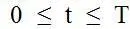, отнесенных к определенным временам осреднения и сопоставление их с соответствующими границами допуска, отнесенными к тем же самым временам осреднения.

Оценки экстремальных значений могут быть сделаны разными способами, в том числе и простым и естественным перебором всех (n) экспериментальных значений, что обычно и делается в производственной практике. На самом деле, это может привести к учету заведомо ошибочных данных, кроме того не дает возможности объективно оценить частоты и вероятности.

Если же промежуток времени между отдельными измерениями ∆t = 0, то метод перебора оправдан, но не позволяет, все-таки, исключить ошибочные и «выскакивающие», то есть не принадлежащие данной статистической совокупности значения. Кроме того, в этом случае, возможно наличие корреляционной связи между членами временного ряда, что ведет к необходимости обработки лишней информации.

Таким образом, во всех случаях целесообразно находить экстремальные значения при помощи какого-либо алгоритма.

У одномерной выборки, состоящей из (n) значений, всегда имеются, по крайней мере, два конечных и однозначно определяемых экстремальных значения и также конечная широта, являющаяся разностью между этими значениями. На первый взгляд кажется, что нахождение экстремума совсем простая задача, достаточно лишь расположить (n) выборочных значений в порядке возрастания их величины и рассмотреть значения, стоящие на i – ом месте от начала или конца (в дальнейшем нас будет интересовать i – е верхнее значение), тогда при получаются экстремальные значения. На самом деле экстремальные значения, как и любая порядковая статистика, обладают выборочной неустойчивостью и определяются свойствами генеральной совокупности, поэтому правильнее их находить по выборке при помощи каких-либо специальных алгоритмов.

Как известно [40], порядковые статистики представляют собой зависимые случайные величины (даже если исходная совокупность независимая) и поэтому описывается некоторым совместным распределением.

Ковариация между i-й и j-й порядковыми статистиками 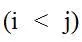вычисляется по формуле:

Следовательно,

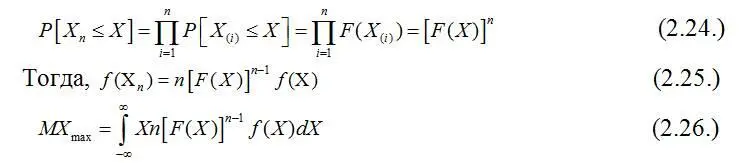
Последнее выражение позволяет оценить X maxесли есть информация о распределении генеральной совокупности. Для нормальной или логнормальной функции распределения, оценки математических ожиданий i – х порядковых статистик могут быть выполнены только численным интегрированием на ЭВМ.