Виктор Назаркин - Атмосфера должна быть чистой. Применение статистических методов при аттестации источников эмиссии и оценке качества атмосферного воздуха

Следуя терминологии математической статистики число (N) можно назвать объемом генеральной совокупности [ 16 ].

Дисперсия среднего арифметического может зависеть от степени связности соответствующих экспериментальных значений 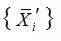[25,26]. Наличие связности между членами временных рядов видимо, впервые было рассмотрено Слуцким [ 25 ]. Им же показано, что устойчивость или связность в рядах затрудняет оценки статистических характеристик и требует оценок корреляционных функций. В настоящее время достаточно хорошо изучена связность метеорологических рядов [27,28], соответственно она должна учитываться в анализе данных о загрязнении воздуха [ 29,30 ]. Если концентрация ЗВ Х(t) в любой момент времени (t), определенная как (2.5.), является случайной величиной, то она однозначно определяется своей функцией распределения вероятности или частоты.

Каждое загрязняющее атмосферу вещество требует вполне определенного времени экспозиции для того, чтобы проявился определенный эффект воздействия. Например, концентрация порога запаха может быть определена органолептически (organoleptical) человеком в течение 1 – 2 сек [ 34 ]. С другой стороны требуется гораздо большее время экспозиции для окиси углерода (СО), чтобы вызвать определенные эффекты в расстройстве здоровья людей. Растения могут быть повреждены при времени экспозиции менее 1 часа, если концентрация (SO 2) или (NO 2) достаточно высока. Таким образом, для того, чтобы связать эффекты воздействия загрязнителей атмосферы с их концентрациями, последние должны быть проанализированы как функции времени экспозиции. Это может быть сделано осреднением концентрации за некоторые периоды времени. В работе [35] приводятся зависимости между 8-часовыми уровнями концентрации (СО) в воздухе и уровнями (СО) в крови. Отмечена очень хорошая корреляция процессов. В то же время, отмечено, что 1 – часовые уровни концентрации (СО) являются плохими индикаторами содержания (СО) в крови, так как последние регулируются достаточно медленными процессами сорбции и десорбции.

Частота, с которой данная концентрация ингредиента может быть превышена, определяет частоту с которой может ожидаться определенный эффект воздействия. Таким образом, для того чтобы связать концентрации с их воздействием, данные о качестве воздуха должны быть проанализированы как функции времени осреднения и частоты.

Долгое время господствовало убеждение, что вполне случайное распределение должно быть строго симметричным и всякую асимметрию считали признаком тенденции к преимущественному появлению односторонних значений и, следовательно, признаком наличия каких-то связей, исключающих случайность. На самом деле это не так. Нетрудно показать, что любая функция случайной переменной, и любая функция распределения может быть преобразована в функцию распределения заданной формы. Нет никаких специальных оснований полагать, что именно тот, а не другой аргумент целиком управляет явлением.

Так как значения ПДК для многих ЗВ весьма малы и находятся на границе чувствительности многих методов и приборов, ошибки измерений резко возрастают. Возможность появления больших средних квадратичных отклонений данных измерений, не зависимо от причин их генерирующих, и как следствие появление больших ошибок вычисления средних (больших 100%) приводит к необходимости использования несимметричных доверительных интервалов и несимметричных функций распределения вероятности.

В частности, такие функции должны быть ограничены слева значением 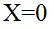во избежание появления бессмысленных с физической точки зрения оценок вида:

Для аппроксимации функции распределения случайных величин Х, изменяющихся на конечном интервале 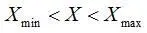предлагалось использовать их разложение по системе ортогональных полиномов Лежандра и Лагерра [ 37 ].

Аналогично, предлагалось использовать разложение по полиномам Лагерра.

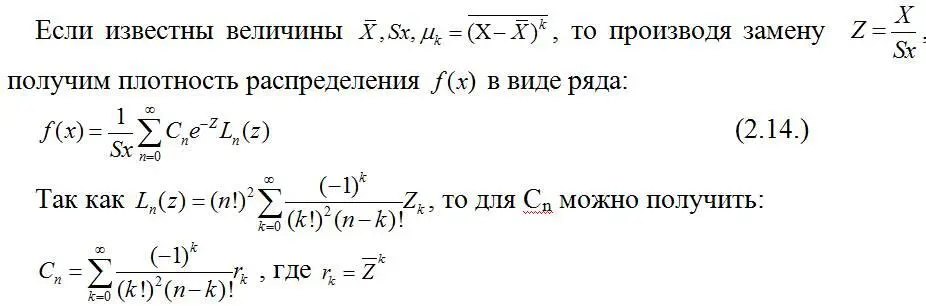
Данный подход универсален и позволяет получить достаточную 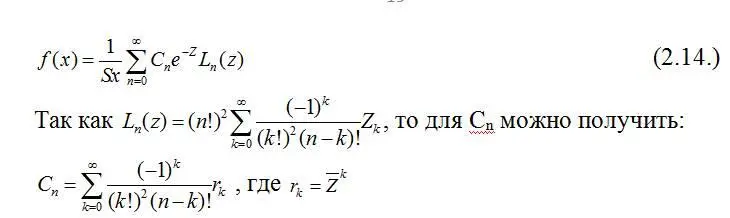точность уже при вычислении 4÷5 членов разложения. Известны и другие виды разложений по ортогональным полиномам, основанным на нормальном распределении. Это, так называемые, ряд Грамма-Шарлье и асимптотическое распределение Эдокворта [ 38 ].

К недостаткам этих представлений следует отнести относительную сложность расчетных процедур и необходимость вычисления лишних моментов и семиинвариантов, так как не учет моментов 5-го и 6-го порядка приводил к генерации отрицательных частот [5].

К недостаткам таких аппроксимаций можно отнести и существенное влияние ошибок в определении параметров реальных распределений.

В последнее время появился ряд убедительных свидетельств в пользу возможности использования логарифмически нормального распределения для выравнивания распределения частот данных о загрязнении воздуха [22,23,39,51].

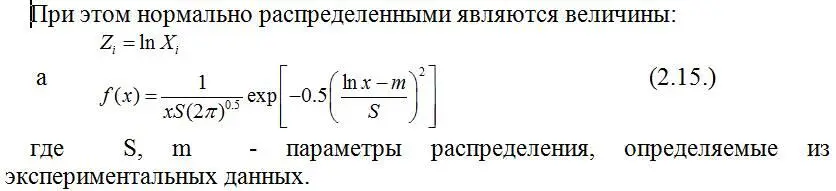
Характерной особенностью логнормального распределения является зависимость дисперсии от математического ожидания, таким образом, что коэффициент вариации остается близким к единице (рис. 2.4.).