Александр Полулях - Тяжелосредное обогащение углей

Из рис. 1.27 видно, что в данном случае плотность разделения δ рравна 2 г/см 3, т. е. 50 % фракции этой плотности перешло в концентрат, а 50 % – в породу.

Так как кривые разделения Т к и Т псимметричны, то ординаты любой точки кривой Т к (или Т п) можно определить как разность 100 минус ордината точки кривой Т п(или Т к ) с той же абсциссой. Поэтому обычно принято графически изображать кривую разделения для тяжелого продукта: в случае разделения исходного угля на два продукта – кривую для породы, а при разделении на три продукта – для породы и для промпродукта. Ордината любой точки кривой разделения Т п(или Т к ) показывает, какая часть бесконечно малой фракции исходного угля, соответствующей этой ординате, перешла в породу (или промпродукт).

При разделении исходного угля на три продукта имеем две плотности разделения (отсечки) – высокую и низкую. Первая соответствует разделению исходного на породу и смесь концентрата с промпродуктом, а вторая – разделению этой смеси на концентрат и промпродукт. Расчет разделительных чисел для промпродукта (при разделении на концентрат и промпродукт) можно производить двумя способами. По первому способу за исходное принимается сумма отдельных фракций (к исходному), содержащихся в концентрате и промпродукте, без породы, выделенной при первом разделении.

Разделительные числа рассчитываются как частное от деления количества определенных фракций в промпродукте к суммарному количеству этих же фракций в концентрате и промпродукте.

В общем виде

где n м – разделительные числа для промпродукта; γ м – содержание определенных фракций в промпродукте от исходного; γ к – содержание тех же фракций в концентрате от исходного.

Этот способ расчета принят в ФРГ.

По второму методу разделительные числа для промпродукта рассчитываются как частное от деления суммарного количества определенных фракций в промпродукте и породе к количеству этих же фракций в исходном угле:

Этот метод расчета принимается во Франции.

В табл. 1.25 и на рис. 1.28 приведены данные по разделению угля на три продукта, результаты расчета разделительных чисел и определения плотностей разделения по обоим способам. Из этих данных видно, что разница в значениях разделительных чисел по первому и второму методу и отклонения кривых являются незначительными, а плотность разделения между концентратом и промпродуктом остается постоянной. Теоретически первый метод расчета и построения кривой разделения второй отсечки является более правильным.

Таблица 1.25

Разделительные числа при разделении исходного угля на три продукта

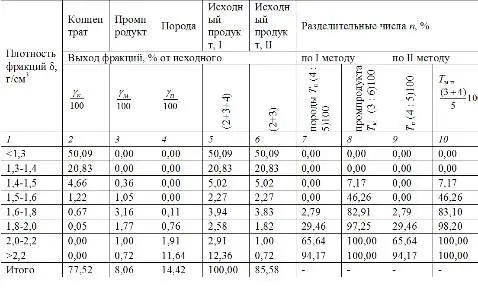
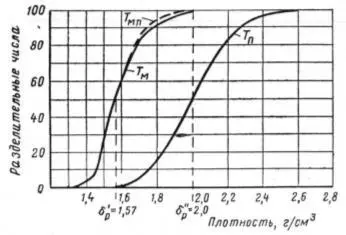
Рис. 1.28. Кривые разделения Т п, Т м; Т м .п

Вероятное отклонение кривой разделения определяется как полуразность между абсциссами (плотностями) точек кривой, соответствующими ординатам (разделительным числам) 25 и 75:

Вероятное отклонение измеряется в единицах плотности на абсциссе кривой разделения.

Для результатов разделения, изображенных на рис. 1.28. вероятное отклонение при δ ' p =2,0 г/см 3

Это означает, что среднее вероятное отклонение плотности посторонних фракций в продуктах обогащения от плотности разделения составляет 0,155 (или 155 кг/м 3). По законам вероятности максимальное отклонение плотности посторонних фракций от плотности разделения составляет

±4 E pm =±4·0,155=±0,62, т. е. если δ p =2 см 3и E pm = 0,155,

то в концентрат могут попасть фракции с плотностью до δ p +4 E pm =2+0,62=2,62 г/см 3, а в породу – фракции с плотностью до δ p -4 E pm =2–0,62=1,38 г/см 3. В интервале от δ p до δ p +4 E pm в продуктах обогащения будут и фракции с промежуточной плотностью.

Чем меньше среднее вероятное отклонение обогатительного аппарата, т. е. чем меньше среднее отклонение плотности посторонних фракций в продуктах обогащения от плотности разделения, тем лучше и точнее работает этот аппарат. Величина Е pm определяет угол наклона кривой разделения к вертикали: чем меньше Е pm тем меньше этот угол, и если Е pm = 0, то α = 0 кривая разделения превращается в вертикальную линию, что свидетельствует об идеальном разделении угля.

Установлено, что величина вероятного отклонения в значительной степени зависит от крупности обогащаемого угля и от плотности разделения.

Данные, иллюстрирующие это положение, приведены в табл. 1.26 и 1.27 [75].

При обогащении угля одинаковой крупности среднее вероятное отклонение повышается по мере возрастания плотности разделения. Это увеличение незначительно для обогатительных машин с тяжелой средой и существенно для машин с водной средой. По этой причине для машин с водной средой оценка эффективности разделения производится не по Е pm как для аппаратов с тяжелой средой, а по безразмерному коэффициенту погрешности J :

где δ p – плотность разделения, г/см 3.

Таблица 1.26

Значения для некоторых аппаратов

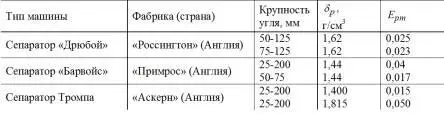
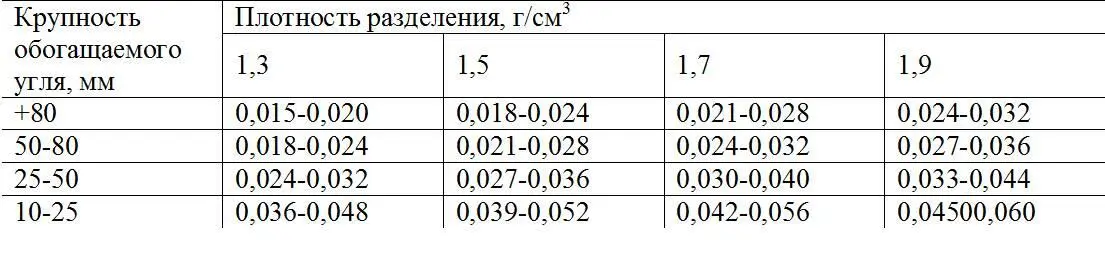
Таблица 1.27

Значения для аппаратов с тяжелой суспензией

Этот коэффициент позволяет судить о точности работы обогатительной машины независимо от плотности разделения.

Многие исследователи, так же как и авторы метода оценки эффективности разделения по Е pm считают, что для одной и той же обогатительной машины этот показатель и форма кривой не зависят от обогатимости угля и, следовательно, для угля одной и той же крупности полностью характеризуют работу данного аппарата.

Однако получение одинаковых значений показателя Е pm для углей различной обогатимости (различного фракционного состава) не означает, что количество элементарной посторонней фракции и общее их количество в полученных продуктах обогащения является также постоянным.