Александр Полулях - Тяжелосредное обогащение углей

для ламинарного режима

для турбулентного режима

Однако такое приближенное рассмотрение не раскрывает механизма разделения зерен и причин взаимного засорения продуктов обогащения. Более реальная картина может быть получена только при учете сил турбулентного перемешивания.

О.Н. Тихонов показал, что эффективность разделения, которую можно характеризовать средним вероятным отклонением Е pm , функционально зависит от отношения усредненной скорости зерна к коэффициенту микродиффузии (ν‾/B) входящего в вероятностное уравнение типа Фоккера-Планка:

где W – вероятность перехода зерна через границу, расположенную в ванне сепаратора на глубине h от места подачи питания; B – коэффициент диффузионного массопереноса.

Входящая в уравнение (2.11) усредненная скорость движения зерна является функцией ряда параметров:

где τ 0 – предельное напряжение сдвига вязко-пластичной среды (суспензии); остальные обозначения прежние.

Определение величины ν‾ связано с решением дифференциального уравнения движения, учитывающего сумму действующих сил.

Коэффициент макродиффузии В определяется действием двух факторов: макроскопической неоднородностью скорости потока (градиент горизонтальной составляющей скорости по глубине потока в проточной части ванны сепаратора) В 1и турбулизацией суспензии при движении крупных зерен обогащаемого материала В 2. Очевидно, что эти факторы действуют независимо друг от друга и что полный коэффициент диффузионного массопереноса

В принципе такое равенство допустимо, так как при взаимном влиянии указанных возмущений результирующее воздействие может быть учтено введением поправочных коэффициентов

При движении зерен в потоке, имеющем градиент горизонтальной скорости, коэффициент диффузионного массопереноса (называемый в этом случае иногда турбулентной вязкостью) может быть выражен как

Таким образом, В 1зависит от максимального размера стационарного вихря h max (он равен или меньше глубины ванны сепаратора), разности максимального ν c. maxи минимального ν c. minзначений скорости потока и коэффициента турбулентной вязкости K .

Объяснением вертикальных перемещений зерен может служить наличие стационарных циркуляций суспензии, переносящих зерна разделившегося материала в ниже- или вышележащие слои. По большей части такие циркуляционные потоки возникают в застойных зонах, т. е. в зонах с пониженной скоростью движения суспензии.

В процессе перемещения в ванне сепаратора за каждым крупным зерном возникает вихревая дорожка, взаимодействие таких вихрей турбулизует весь объем суспензии.

Учитывая, что размер застойных зон, где происходит образование циркуляционных потоков, сопоставим по порядку величин с размером ванны, а размер последней, как правило, на порядок и более превосходит максимальный размер зерна обогащаемого материала, для всех зерен коэффициент В 1можно считать постоянным, зависящим только от гидродинамики потока суспензии в ванне сепаратора. Следовательно, в уравнении (2.12) ξ ≈ 1.

Для коэффициента В 2такое допущение неправомерно, так как линейные размеры турбулентных вихрей, вызываемых движением в ванне зерен обогащаемого материала, сопоставимы с их размером.

Для оценки взаимосвязи турбулентного режима движения суспензии с крупностью зерен обогащаемого материала следует определить размер зерна, для которого вязкостное сопротивление равно профильному.

Из уравнений равенства суммы движущихся сил и сил сопротивления

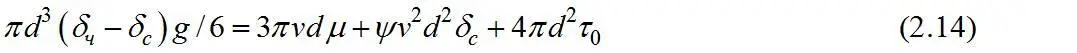
и сил вязкостного и профильного сопротивлений

решенных относительно v (при условии ψ ≈ π /10), получим:

– для вязкостного сопротивления

– для профильного сопротивления

Графическое решение системы уравнений относительно d при характерных параметрах работы тяжелосредного сепаратора ( δ ч– δ с =100 кг/м 3, δ с =2000 кг/м 3, µ =10 -2Па·с, τ 0 =6 н/м 2) дает размер граничного зерна d гр= 15 мм, что близко к нижнему пределу крупности (примерно 13 мм) угля, эффективно обогащаемого в сепараторах.

Для зерен крупностью d ≤ d грпри этих условиях преобладает вязкостное сопротивление, для зерен крупностью d ≥ d гр– профильное сопротивление, т. е. в первом случае в качестве коэффициента диффузионного массопереноса превалирует В 1( В ≈ В 1), во втором – В 2( В ≈ В 2).

Исходя их этих соображений, можно полагать, что при выбранных параметрах процесса энергия турбулентных пульсаций в ванне сепаратора пропорциональна единовременной концентрации материала крупностью более d гр, т. е. дисперсия турбулентных пульсаций D тзависит от производительности сепаратора, гранулометрического и фракционного состава питания, плотности, вязкости и предельного напряжения сдвига суспензии:

где Р( δ ч, d ) – распределение обогащаемого материала по плотности и крупности.

Приняв линейный размер турбулентной пульсации L = d max, можно оценить случайную составляющую скорости турбулентных пульсаций:

где ω(t) – вертикальная скорость потока суспензии, м/с; ω ‾ – среднее значение вертикальной скорости потока, м/с; ν max– максимальная скорость движения частицы размером d max, м/с; K 1 – коэффициент пропорциональности ( K 1 <1);