Петр Силин - Некоторые аспекты оценки эффективности функционирования систем. Вторая редакция, исправленная и дополненная

По мнению автора, можно утверждать, что любой объект любого рода можно описать набором значений характеристик, именуемых параметрами.

Также общеизвестно, что параметры сложных объектов, которые принято именовать макропараметрами, появляются на свет в результате объединения более простых объектов в сложный, в свою очередь более простые объекты описываются своими параметрами, которые в контексте данного анализа можно называть микропараметрами.

Рассматривая окружающий нас мир со всеми существующими в нем объектами, можно отметить для себя, что каждый материальный объект может быть описан тем или иным образом с применением некоторого набора характеристик или параметров.

При этом можно заметить, что, в зависимости от природы объектов, могут изменяться:

– количество используемых для описания параметров,

– типы параметров, свойства параметров (например, дискретность или непрерывность принимаемых значений, численный или качественный характер принимаемых значений и т.д.),

– протяженность интервалов значений, принимаемых каждым параметром,

– различность набора параметров при сравнении ситуаций изолированности объектов от внешнего мира и в случае существования взаимодействия анализируемого объекта с другими объектами (окружающим миром).

Такое многообразие, может быть приятное при других обстоятельствах, в нашем случае только мешает.

Поэтому автор считает возможным для облегчения анализа ввести в рассмотрение объект, используемый исключительно для изучения вопросов о параметрах систем.

Этот объект имеет N параметров, каждый параметр принимает значения в интервале значений, обозначение которого приведено в строке 1 таблицы 1 в разделе 1.10 (далее таблица 1), свойства и природа параметров во внимание не принимаются.

Таковой объект далее будем именовать аналитический объект или просто – Объект.

Введение аналитического объекта позволяет сделать еще один шаг и обратить внимание на ряд явлений, процессов и образований, в том числе и виртуальных, поведение и состояние которых также могут быть отражено набором параметров.

В качестве практического примера аналитического объекта могут быть приняты такие явления как материальные объекты, информационные потоки, информационные контенты, полевые структуры и пр.

В рамках понятия аналитического объекта не проводится дифференциация по нативному происхождению объекта или явления.

Учитывая сказанное, в контексте данных материалов к понятию Объектамогут быть причислены любые материальные объекты, явления и образования любой природы, если они могут быть представлены набором параметров.

Здесь необходимо, по мнению автора, сделать замечание того свойства, что отвлечение от свойств параметров не является большой натяжкой, так как избавиться от особенностей параметров позволяет операция нормализации параметров, рассмотренная ниже в разделе 1.1.1.

1.1.1. Нормализация параметров.

Нормализация параметров, по мнению автора, позволяет избежать необходимости учета индивидуальных свойств параметров при анализе объектов. Нормализация параметров состоит в том, что каждое значение из интервала принимаемых параметром значений относится к минимальному значению из указанного интервала.

В результате применения нормализации ко всем параметрам объекта получим, что каждый параметр становится безразмерным и будет принимать значения внутри интервала от 1 до некоторого максимального значения Y max, normall, определяемого выражением (п 1, промежуточное первое):

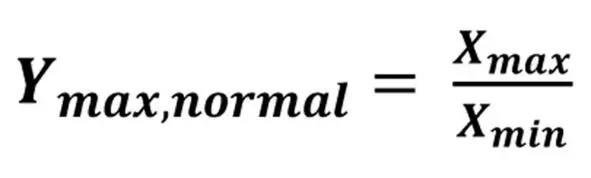
выражение п 1

Такой подход позволяет в дальнейшем обращаться с параметрами объектов и самими объектами совершенно формально, не обращая внимание на их реальную сущность.

В дальнейшем всегда, без специальных оговорок, будут подразумеваться только нормализованные параметры без специального уведомления.

1.1.2. Условные и безусловные параметры.

Параметры, являющиеся имманентными характеристиками объекта, будут именоваться безусловными параметрами.

Свойства, которые не присущи объекту с начала его существования, но в процессе его генезиса, в рамках той или иной задачи, проявляют свое существование и характеризуют объект с той или иной стороны, будут считаться параметрами, если это упрощает решение задачи, но условными или временными. В период, когда эти характеристики считаются параметрами, на них распространяются все «права и обязанности» настоящих параметров.

Определившись с описанием в виде набора нормализованных параметров, следует определиться с представлением наборов параметров и интервалов принимаемых ими значений для облегчения анализа объекта.

Вполне обычным является вариант матричного представления параметров и интервалов их значений. Этот способ, по мнению автора, достаточно очевиден и нагляден, но оперирует только с дискретными значениями параметров. К тому же операции с матрицами не вполне однозначны, хотя и интересны.

Другим широко распространенным вариантом является построение различного рода моделей (абстрактных, натурных, имитационных), манипулирование с которыми позволяет проанализировать объект.

Этот метод также очевиден, распространен, дает наглядные результаты.

Но следует отметить, что не всегда удается построить адекватную модель, к тому же автор полагает, что этот метод должен играть вспомогательную роль при анализе объекта – для подтверждения гипотез или иллюстрации ранее сделанных выводов, например.

Автор, в свою очередь, не отрицая применимости перечисленных методов, склоняется к другому способу отображения параметров. В основу положена система взаимно перпендикулярных координат. Количество осей совпадает с количеством параметров объекта. На каждой оси откладываются интервалы принимаемых значений параметров объекта и сами значения, в случае счетного количества дискретных значений, а в общем случае, непрерывные значения или бесконечное количество дискретных значений. По взаимному расположению значений параметров каждая ось является равномерной шкалой.

В результате этих манипуляций будет получена для объекта с N независимыми параметрами N -мерная система координат, именуемая, в дальнейшем, параметрическим пространством.