Петр Силин - Некоторые аспекты оценки эффективности функционирования систем. Вторая редакция, исправленная и дополненная

Объекты одного типа, имеющие одинаковые контенты состояний являются объектами одного вида.

Объекты разных типов, имеющие какое-либо количество одинаковых параметров, будут именоваться подобными объектами.

Заметим, что если подобные объекты поместить в одно пространство состояний (рабочее глобальное пространство, естественно), то контенты состояний таких объектов будут взаимно пересекаться.

1.2.3. Замечания об изображении объектов.

1.2.3.1. Объекты в пространстве состояний , в зависимости от требований рассматриваемого вопроса, будут изображаться либо в виде точки, иллюстрирующей конкретное состояние объекта, либо в виде вектора, отображая целевые устремления объектов, смещения объектов, информационные потоки.

1.2.3.2. Являясь обычным человеком , автор достаточно легко может представить себе и нарисовать систему координат размерности не более трех. При попытке вообразить большее количество измерений возникают определенные ментальные трудности. Поэтому для иллюстрации поведения объектов в пространстве состояний будет использоваться в основном двумерная система координат, реже – трехмерная.

Думается, что в этом нет большой ошибки либо натяжки, т.к. если изобразить состояние объекта в виде вектора, начинающегося в начале координат и заканчивающегося в точке А , и вектор {OA} имеет N координат, то вполне позволительно свести N-1 координат в одну результирующую координату, а второе измерение образуется N-ной координатой, как показано в выражении (3):

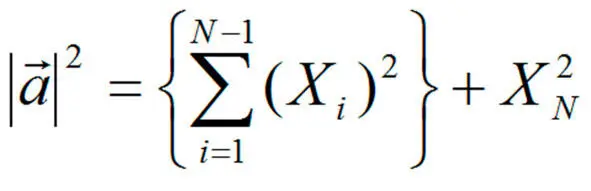
выражение 3

1.2.3.3. Заметим для читателя , что в дальнейшем для иллюстрации будет использоваться дискретный контент состояний, ибо, по мнению автора это будет наиболее выразительно с точки зрения иллюстративности.

Объект, подвергаемый изучению, не только существует в пространстве состояний, но и движется в нем. Движение в пространстве состояний несколько отличается от привычного для нас движения объектов в пространстве, ибо не всегда подразумевает физическое перемещение объекта в Евклидовом пространстве.

Движение объекта в пространстве состояний в общем случае отражает процесс изменения состояния объекта.

Рисунок 4. Движение в пространстве состояний

Движение в пространстве состояний может быть вызвано различными причинами – целенаправленным или случайным воздействием окружающего мира, воздействием системы управления объекта, различного рода трансформациями и модификациями самого объекта.

Но каковы бы не были причины, вызывающие движение рассматриваемого объекта в пространстве состояний, состояние рассматриваемого объекта, очевидно, изменяется в результате изменения текущих значений параметров объекта.

Таким образом, напрашивается вывод – чтобы вызвать смещение объекта в пространстве состояний, следует произвести соответствующее изменение значений параметров объекта, то есть необходимо воздействовать на параметры.

Полученный вывод позволит в дальнейшем, при помощи пространства состояний, свести анализ объектов к анализу параметров объектов.

Остальные аспекты пространства состояний объектов и движения объектов в указанном пространстве рассматриваются ниже.

1.3.1. Векторы смещения, цели, коррекции и новых устройств, минимальный уровень воздействия.

Как указывалось ранее, при воздействии на объект со стороны окружающей среды или системы его управления объект переходит в другое состояние. Между начальным и конечным состояниями в пространстве состояний образуется некоторое расстояние, которое будем именовать смещением. Величина смещения может быть исчислена с помощью вектора, который образуется как направленный отрезок между начальным и конечным состояниями объекта.

1.3.1.1. Одиночное воздействие

Обратимся к рисунку 5.

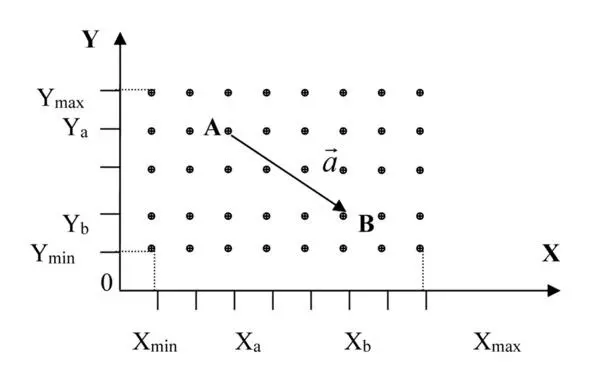
Рисунок 5. Вектор смещения

На рисунке изображено смещение объекта из состояния A (Xa, Ya) в состояние B (Xb, Yb) в результате одиночного воздействия.

При переходе объекта из одного состояния в другое соответствующим образом изменяются значения его параметров, впрочем, верно и обратное утверждение.

Величина смещения определяется длиной отрезка [AB] .

В свою очередь, при учете направления смещения, отрезок [AB] становится вектором {a} , длина которого определяет величину смещения, а направление вектора {a} определяет направление смещения рассматриваемого объекта в пространстве состояний.

Длина вектора {a} определяется как сумма квадратов разниц начальных и конечных координат смещения по всем параметрам, т.е.:

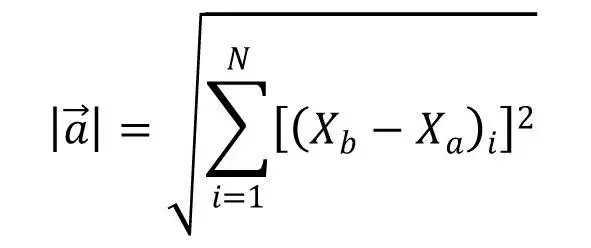
выражение 4.1

где X b и X a – соответственно конечные и начальные значения i-того параметра, количество которых составляет N .

Формула (4.1) позволяет определить величину смещения объекта в пространстве состояний в общем случае.

Формула (4.2) позволяет определить направление смещения объекта в пространстве состояний в общем случае:

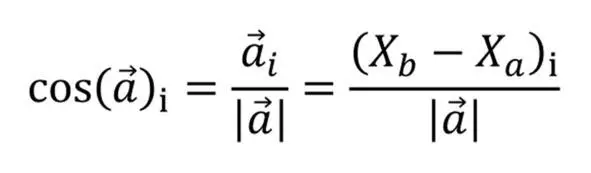
выражение 4.2

Как любой вектор, вектор смещения обладает определенными координатами. Как видно из рисунков 6, формул (1—4), правил сложения векторов (если начальное и конечное состояния изобразить в виде соответствующих векторов) координаты вектора смещения определяются как разница начальных и конечных значений соответствующих параметров, т.е. можно записать выражение (5) для вектора смещения:

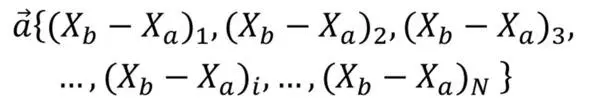
выражение 5

где X b и X a – соответственно конечные и начальные значения i-того параметра, количество которых составляет N .