О. ОРЕ - Приглашение в теорию чисел

Из этого обсуждения мы можем сделать вывод: любые два натуральных числа а и b имеют наибольший общий делитель d 0. Простыми множителями p i числа d 0являются те, которые одновременно встречаются в числах а и b , а степень числа р i в числе d 0есть меньшее из двух чисел α i и β i .

Пример. Возьмем два числа, указанных в (4.1.2), имеющие разложения на простые множители (4.1.3); очевидно, что

d 0= 2 15 1= 10.

Так как степень простого числа p i в наибольшем общем делителе по крайней мере не меньше, чем у любого другого общего делителя, то мы получаем характеристическое свойство:

Любой общий делитель d делит наибольший общий делитель d 0.

Наибольший общий делитель двух чисел настолько важен, что для него существует специальное обозначение:

d 0= D ( a, b ). (4.1.4)

Система задач 4.1.

1. Найдите наибольший общий делитель пар чисел: а) 360 и 1970, б) 30 и 365, в) номера вашего телефона и вашего почтового индекса.

2. Как бы вы стали доказывать, что √2 есть иррациональное число, используя в доказательстве теорему о единственности разложения?

Число 1 является общим делителем для любой пары чисел а и b . Может случиться, что единица будет единственным их общим делителем, т. е.

d 0= D ( a, b ) = 1. (4.2.1)

В этом случае мы говорим, что числа а и b взаимно простые.

Пример. (39, 22) = 1.

Если числа имеют общий делитель, больший единицы, то они также имеют общий простой делитель.

Итак, два числа могут быть взаимно простыми только тогда, когда они не имеют общих простых множителей, поэтому условие (4.2.1) означает, что числа а и b не имеют общих простых множителей, т. е. все их простые множители различны.

Вернемся к началу этой главы, где мы приводили дробь а / b к простейшему виду. Если d 0есть наибольший общий делитель чисел а и b , то мы можем написать

a = a 0 d 0, b = b 0 d 0. (4.2.2)

Тогда

a/b = a 0 d 0 /b 0 d 0= a 0 /b 0. (4.2.3)

В формуле (4.2.2) числа а 0и b 0не могут иметь простых общих множителей, в противном случае числа а и b имели бы общин множитель, больший, чём d 0. Следовательно,

D(a 0, b 0) = 1. (4.2.4)

Это означает, что для второй дроби в формуле (4.2.3) дальнейшее сокращение невозможно.

Одним из часто применяемых свойств взаимно простых чисел является следующее.

Если произведение ab делится на число с, которое взаимно просто с числом b, то число а делится на с.

Доказательство. Так как число с делит произведение ab , то простые множители числа с содержатся среди простых множителей чисел а и b . Но так как D ( b, c ) = 1, то их не может быть среди множителей числа b . Таким образом, все простые множители числа с делят число а , но не делят число b , и они появляются в числе а в степенях, не меньших, чем в числе с , так как число с делит ab .

Позже мы используем другой факт.

Если произведение двух взаимно простых чисел является квадратом,

ab = c 2 , D ( a, b ) = 1, (4.2.5)

то числа а и b являются квадратами:

а = а 1 2 , b = b 1 2. (4.2.6)

Доказательство. Для того чтобы некоторое число было квадратом, необходимо и достаточно, чтобы все степени в разложении его на простые множители были четными. Так как числа а и b — взаимно простые (4.2.5), то любой простой множитель из с 2содержится либо в а , либо в b , но не в обоих; отсюда простые множители чисел а и b должны иметь четные степени.

Система задач 4.2.

1. Какие числа взаимно простые с числом 2?

2. Почему D ( n, n + 1) = 1?

3. Исследуйте пары дружественных чисел в табл. 2 (стр. 45) и найдите те из них, которые взаимно просты.

4. Может ли правило, выраженное в формулах (4.2.5) и (4.2.6), быть справедливым не только для квадратов, но и для произвольных степеней?

Вновь вернемся к нашим дробям а / b . Если а > b , то дробь является числом, большим 1, и мы часто разделяем ее на целую часть и правильную дробь, меньшую единицы.

Примеры . Мы пишем

32/5 = 6 + 2/5 = 6 2/5, 63/7 = 9 + 0/7 = 9.

В общем случае мы используем деление с остатком

чисел а и b ( a ≥ b ), а именно:

a = qb + r , где 0 ≤ r ≤ b —1. (4.3.1)

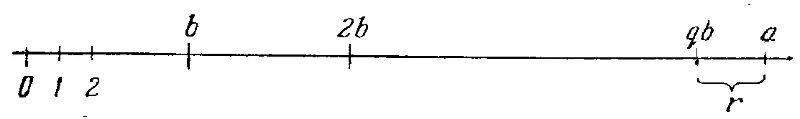
Рис. 14.

Очевидно, что это всегда возможно. Действительно, рассмотрим числа 0, 1, 2… на числовой прямой (рис. 14). Где-то на этой прямой расположено число а . Начиная от точки 0 станем отмечать точки b , 2 b , З b и т. д. до точки qb такой, что qb не больше, чем а , в то время как ( q + 1) b уже больше а . Расстояние от точки qb до точки а и есть r . Мы называем число r остатком при делении (4.3.1), a q — частным . Это частное q встречается столь часто, что имеется специальный символ для его обозначения:

q = [ a/b ].

Этот символ обозначает наибольшее целое число, не превосходящее числа а/b . Для примеров, приведенных выше, получим

[32/5] = 6, [63/7] = 9.

В предыдущем разделе мы исследовали наибольший общий делитель двух натуральных чисел а и b :

d 0= D ( a, b ). (4.3.2)

Чтобы найти число d 0, мы полагали, что мы знаем разложения чисел а и b на простые множители. Однако нахождение таких разложений может оказаться очень трудным занятием для больших чисел. Существует совсем другой метод для нахождения наибольшего общего делителя, который не использует подобных разложений. Он основан на следующем:

Если a = qb + r, где 0 ≤ r ≤ b—1, то

D(a, b) = d = D(r, b). (4.3.3)

Доказательство. Запишем

d 0= D ( a, b ), d 1= D(r, b).

Таким образом, доказательство соотношения (4.3.3) означает доказательство того, что d 0= d 1. Любой общий делитель чисел а и b также делит число

r = а — qb .

Следовательно, число r делится на d 0.

Так как число d 0является делителем как числа r , так и числа b , то оно должно делить и число d 1= D ( b, r ); отсюда d 1≥ d 0. С другой стороны, в соответствии с соотношением (4.3.1) любой общий делитель чисел r и b делит число а , откуда число d 1делит число а . Так как число d 1делит также и число b , то оно должно делить и число d 0= D ( a, b ), следовательно, d 0≥ d 1. Из сказанного следует, что d 0= d 1.