О. ОРЕ - Приглашение в теорию чисел

S N + M ≡ S N + S M (mod 9), (8.1.3)

т. е. количество фишек, находящихся на доске, должно отличаться от первоначального общего числа фишек на число, кратное 9. Эта проверка (8.1.3) до сих пор сохранила свое старое название «выбрасывание девяток».

После того как это правило было открыто, не составило труда заметить, что оно также применимо при сложении нескольких чисел, при вычитании и при умножении; в последнем случае, в соответствии с (8.1.3),

S MS N ≡ S MN (mod 9). (8.1.4)

Теоретическое доказательство этих правил является легкой задачей при использовании сравнений. Очевидно, что

1 ≡ 1, 10 ≡ 1, 10 2≡ 1, 10 3≡ 1… (mod 9); (8.1.5)

таким образом, из (8.1.1) и (8.1.2) мы делаем вывод, что

N ≡ S N (mod 9). (8.1.6)

Поэтому из правил сравнений, которые мы установили в § 3 главы 7, ясно, что

S N ± S M ≡ N ± М ≡ S N ± M ,

S N • S M = N • M ≡ S N • M (mod 9).

Правило «выбрасывания девяток» чаще всего применяется к умножению. Возьмем в качестве примера числа

M = 3119, N = 3724 (8.1.7)

и их произведение

М • N = 11 614 156.

Это вычисление не может быть верным, так как если бы оно было верным, то мы имели бы, что

M ≡ S M ≡ 3 + 1 + 1 + 9 ≡ 5 (mod 9),

N ≡ S N ≡ 3 + 7 + 2 + 4 ≡ 7(mod 9)

и MN ≡ S MN ≡ 1 + 1 + 6 + 1 + 4 + 1 +5 + 6 ≡ 7 (mod 9).

Но 5 • 7 = 35 ≠ 7 (mod 9).

В действительности же это произведение равно MN = 11 615 156.

В средневековых школах ученики имели строгий наказ обязательно проводить проверку своих упражнений. Поэтому в рукописях, сохранившихся с тех времен, мы видим множество знаков, похожих на эмблему из скрещенных костей. Такой знак для нашего примера выглядит так, как на рис. 18.

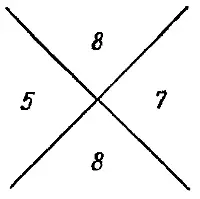
Рис. 18.

Здесь числа 5 и 7, лежащие слева и справа, означают остатки чисел М и N (по модулю 9), а верхнее число 8 является остатком вычисленного произведения MN . Оно должно проверяться с помощью произведения остатков начальных чисел, записываемого в нижней части.

Здесь

5 • 7 = 35 ≡ 8 (mod 9).

Рис. 19.

Такая проверка «скрещенных костей» была совершенно обычной в ранних изданиях учебников арифметики (рис. 19), например, в английских учебниках семнадцатого и восемнадцатого веков. Конечно, существует возможность, что вычисления содержат ошибку, необнаруживаемую методом «выбрасывания девяток», но тогда мы знаем, что ошибка является «ошибкой по модулю 9».

Ясно, что и при другом основании системы счисления можно использовать простейшую проверку. Для числа

M = m nb n + m n -1 b n -1+… + m 2 b 2+ m 1 b + m 0,

записанного при основании b , как и в (8.1.5), мы имеем

1 ≡ 1, b ≡ 1, b 2 ≡ 1… (mod ( b — 1));

поэтому, как и раньше,

М ≡ S M = m n + m n -1+… + m 2+ m 1+ m 0(mod ( b — 1)),

и проверочное правило остается прежним.

Это, по-видимому, совершенно тривиальное замечание применимо даже в нашей обычной десятичной системе. Мы упоминали в § 5 главы 7, что если мы разобьем цифры десятичного числа на группы по три, то тогда эта группировка может рассматриваться как представление числа при основании b = 10 3= 1000. Аналогично, если группировать цифры в пары, то это соответствует представлению числа при основании b = 10 2= 100.

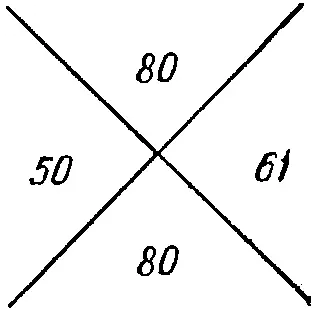
Рис. 20.

Взяв числа 3119 и 3724 вновь в качестве примера и записав

M = 31 19, N = 37 24, MN = 11 61 51 56,

мы находим

M ≡ 31 + 19 = 50 (mod 99), N ≡ 37 + 24 = 61 (mod 99),

MN ≡ 11 +61+ 51+56 = 179 ≡ 80 (mod 99).

Здесь наша проверка «скрещенных костей» будет такой, как на рис. 20, потому что, как легко видеть, 50 • 61 ≡ 80 (mod 99).

Эта проверка более эффективна, чем «выкидывание девяток», потому что модули в этом случае гораздо больше и вероятность, что ответ будет правильным, соответственно гораздо больше. Другими словами, «ошибка по модулю 99» менее вероятна, чем «ошибка по модулю 9».

Многие задачи астрономии и хронологии, связанные с периодичностью, могут быть сформулированы в терминах теоретико-числовых понятий. Возьмем простой пример: определение дня недели, который падает на заданный день. Дни недели повторяются с периодом 7, поэтому вместо обычных названий мы можем дать каждому дню номер:

воскресенье = 0,

понедельник = 1,

вторник = 2,

среда = 3,

четверг = 4,

пятница = 5,

суббота = 6.

Если мы это сделаем, то каждому целому числу соответствует день недели, а именно: день, определяемый его остатком по модулю 7.

Если бы мы имели благоприятнейшую ситуацию, при которой количество дней в году делилось на 7, то все даты падали бы на одни и те же дни ежегодно, и составление расписаний было бы гораздо проще, а издатели календарей имели бы меньше работы. Однако количество дней в году равно

365 ≡ 1 (mod 7),

за исключением високосных лет, в которых количество дней

366 ≡ 2 (mod 7).

Это показывает, что для обычного года номер W дня недели заданной даты в следующем году увеличится на 1, например, если в этом году 1 января — воскресенье, то в следующем году он будет падать на понедельник. Это не слишком сложно, однако, эта простая схема нарушается високосными годами. Это происходит каждый четвертый год, тогда номер дня недели увеличивается на 2. Более того, возникает дополнительная трудность из-за того, что добавочный день високосного года прибавляется не в начале или конце года, а 29 февраля. Поэтому, для удобства, в общей формуле для вычисления W, которую мы дадим ниже, договоримся считать март — первым месяцем, апрель — вторым и т. д., при этом январь будет одиннадцатым месяцем, а февраль — двенадцатым месяцем предшествующего года.

Но на этом наши трудности не кончаются. В юлианском календаре, введенном по указу Юлия Цезаря, было принято, что год точно равен 365 1/4 дня, в соответствии с правилом високосного года. Однако это не совсем правильно, так как астрономический год в действительности равен 365,2422 дня.

Эта маленькая ошибка вызвала постепенный сдвиг сезонов по отношению к календарю, например, в шестнадцатом веке день весеннего равноденствия (первый день весны) пал на 11 марта вместо 21 марта, как это должно было быть.

Чтобы исправить положение, в 1582 году папа Григорий XIII после долгих колебаний произвел реформу календаря в странах с католическим вероисповеданием. В том году было опущено 10 дней, а именно, пятницу 5 октября стали считать пятницей 15 октября. Более того, для корректирования календаря были введены следующие григорианские правила для високосных лет.