Елена Замедлина - Статистика. Шпаргалка

Преднамеренные и непреднамеренные ошибки определяются степенью тенденциозности подхода к установлению факта. Преднамеренные ошибкивыражаются в сознательном искажении значений признаков. Непреднамеренные ошибкивозникают независимо от сознания людей, участвующих в статистическом наблюдении.

Для выявления ошибок наблюдения применяют следующие виды контроля:

1) счетный контроль.Заключается в проверке итогов подсчета данных, а также в использовании количественных связей между показателями;

2) логический контроль.Осуществляется путем проверки содержательной связи между значениями признаков. При логическом контроле отыскиваются недопустимые отклонения значений признака от наиболее вероятных.

Выборочное наблюдение– это такое наблюдение, при котором обследованию подвергается часть единиц изучаемой совокупности, отобранных на основе научно разработанных принципов, обеспечивающих получение достаточного количества достоверных данных для характеристики совокупности в целом.

Основные принципывыборочного наблюдения следующие: случайность отбора наблюдаемого явления; репрезентативность выборки.

В основе принципа случайности лежит равная возможность для каждой единицы попасть в выборку. Репрезентативные выборки обеспечивают достаточным числом отобранных единиц. Средние и относительные показатели, полученные на основе выборочных данных, должны достаточно полно воспроизводить или представлять соответствующие показатели совокупности в целом.

Выборочное наблюдение предполагает проведение таких этапов, как:

1) определение объекта и целей выборочного наблюдения;

2) выбор схемы отбора единиц наблюдения;

3) расчет объема выборки;

4) проведение случайного отбора установленного числа единиц из генеральной совокупности;

5) наблюдение отобранных единиц по установленной программе;

6) расчет выборочных характеристик в соответствии с программой выборочного наблюдения;

7) определение ошибки, ее размера;

8) распространение выборочных данных на генеральную совокупность;

9) анализ полученных данных.

Выборочное наблюдение имеет следующие основные преимущества и недостатки:

1) преимущества:

а) его можно осуществить по более широкой программе;

б) его требует меньше затрат на проведение;

в) его организуют в тех случаях, когда невозможно воспользоваться отчетностью;

2) недостатки:

а) полученные данные всегда содержат ошибку;

б) о результатах наблюдения можно судить лишь с определенной степенью достоверности.

Вся совокупность единиц, из которых производится отбор, называется генеральной совокупностью.Часть единиц генеральной совокупности, отобранная в случайном порядке, составляет выборочную совокупность.Характеристиками генеральной и выборочной совокупности служат доля и средняя величина, а также дисперсия и среднее квадратическое отклонение. Средняя величина является характеристикой количественных признаков, а дол я – характеристикой альтернативных признаков.

Среднее значение признака генеральной совокупности называется генеральной средней, обозначается 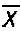, выборочной совокупности – выборочной средней, обозначается .

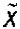Доля генеральной совокупности называется генеральной долей и обозначается р, доля выборочной совокупности называется выборочной долей и обозначается w. Численность генеральной совокупности обозначается N, а численность выборочной – n.

Ошибка выборки – расхождение между характеристиками выборки и характеристиками генеральной совокупности. Она зависит от ряда факторов: степени вариации изучаемого признака, численности выборки, методов отбора единиц в выборочную совокупность, принятого уровня достоверности результата исследования. Ошибка выборки состоит из ошибки регистрации и ошибки репрезентативности, которые бывают систематическими и случайными.

Систематические ошибки связаны с неправильной организацией и имеют тенденцию накапливаться. Случайные ошибкивозникают вследствие того, что выборка недостаточно точно воспроизводит всю совокупность.

Ошибка репрезентативностиобусловлена отличием структуры выборки от структуры генеральной совокупности. Чем больше единиц отобрано из генеральной совокупности, тем меньше ошибка выборки. Чем сильнее вариация, тем больше ошибка выборки.

Определение ошибки выборочной средней.При случайном повторном отборе средняя ошибка выборочной средней рассчитывается по формуле: 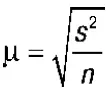, где s 2– дисперсия выборки; n – численность выборки.

При бесповторном отборе она рассчитывается по формуле: 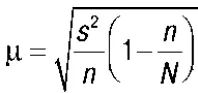, где N – численность генеральной совокупности.

Определение ошибки выборочной доли.При повторном отборе средняя ошибка выборочной доли рассчитывается по формуле:

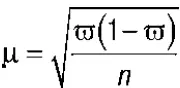
где 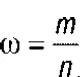– выборочная доля;

m — число единиц, обладающих изучаемым признаком; n — численность выборки.

При бесповторном способе отбора средняя ошибка выборочной доли определяется по формуле:

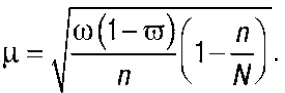
Предельная ошибка выборки Δ связана со средней ошибкой выборки μ отношением: Δ = t × μ .

При этом t как коэффициент кратности средней ошибки выборки зависит от значения вероятности Р, с которой гарантируется величина предельной ошибки выборки.

Предельная ошибка выборки при бесповторном отборе определяется по формулам:

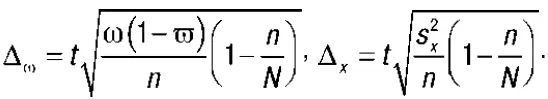
Предельная ошибка выборки при повторном отборе определяется по формулам:

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.