Роман Сиренко - Сопротивление материалов. Шпаргалка для студентов

Соответственно видам внутренних силовых факторов различают четыре вида деформаций тела:

– если в сечении имеется только продольная сила – растяжение или сжатие;

– если в сечении возникают только поперечные силы – с двиг;

– если в сечении возникают только изгибающие моменты – чистый изгиб, если кроме изгибающих моментов возникают поперечные силы – поперечный изгиб;

– если в сечении возникает крутящий момент – кручение.

Если в сечении действуют несколько силовых факторов, то возникает сложный вид деформации.

Как уже было сказано, при определении внутренних сил методом сечения считаем эти силы приложенными к центру тяжести сечения. На самом деле они распределены по всей поверхности сечения, и интенсивность внутренних силовых факторов может быть различной. Увеличение внешней нагрузки приводит к увеличению внутренней, заставляет возрастать интенсивность во всех точках сечения и может привести к разрушению элемента или возникновению остаточных деформаций. Таким образом, говоря о прочности тела, рассматривать надо не значение внутренних сил, а их интенсивность. Меру интенсивности внутренних сил характеризует напряжение.Для удобства математического и физического анализа напряжение рассматривают как совокупность двух компонент: вектора нормального напряжения и вектора касательно напряжения, являющихся соответственно его составляющими по нормали к сечению и касательно к его плоскости.

Рассмотрим небольшую площадку сечения некоторого тела, действующую на нее; внутреннюю силу обозначим Δ F . Отношение внутренней силы к единице площадки определяет среднее значение интенсивности на площадке Δ A .

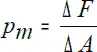
Если бесконечно уменьшать площадку Δ A , напряжение стремится к своему предельному значению и называется истинным напряжением.

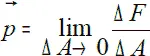
Разложим вектор полного напряжения p на две составляющие: нормальное напряжение σ , направленное по нормали к сечению, и касательное напряжением τ , направленное по касательной к сечению. Между величинами p, τ, σ существует зависимость, которая выражается формулой:

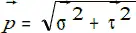
Нормальные напряжения возникают, когда под действием внешних сил частицы стремятся приблизиться или отдалиться. Когда частицы стремятся сдвинуться относительно друг друга в плоскости сечения. Касательное напряжение можно разложить на две составляющие: τ zx и τ zy . Первый индекс показывает, какая ось перпендикулярна сечению, второй – параллельно какой оси действует напряжение.

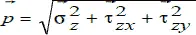
Напряжения в поперечных сечениях связаны с внутренними силовыми факторами, определенными зависимостями.

dN z= σ zdA; dQ x = τ zxdA; dQ y = τ zydA

Соответствующие элементарные моменты относительно координатных осей имеют вид:

dM z = ( τ zxdA ) y – ( τ zydA ) x; dM x = ( σ zdA ) y;dM y =( σ zdA ) x

Просуммировав бесконечно малые силы и моменты, действующие в сечении, получим выражения, связывающие внутренние силовые факторы с напряжениями.

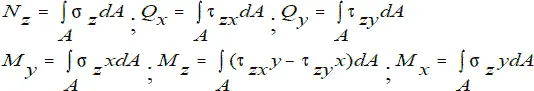
Полученные выражения можно рассматривать как определения, выражающие физическую сущность внутренних силовых факторов. Также, при определенных методах сечения внутренних факторов, эти формулы могут использоваться для вычисления напряжений, если известны законы, по которым эти напряжения распределяются по сечению.

Некоторые элементы конструкций и элементов подвергаются только продольным нагрузкам, что вызывает в них деформацию растяжения или сжатия. Длина стержня, подвергнутого растяжению, увеличивается, а площадь его поперечного сечения уменьшается. При сжатии наоборот – длина уменьшается, а площадь сечения увеличивается. При этом изменение длины называют линейной продольной деформацией, а изменение площади поперечного сечения – поперечной линейной деформацией. Для оценки интенсивности деформации применяют такие понятия, как относительная продольная ε и относительная поперечная ε' – деформации, приходящиеся на единицу длины или пощади сечения стержня.

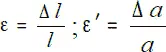
где Δ l – изменение длины стержня;

Δ a – изменение площади сечения.

Продольную деформацию растяжения обычно считают положительной, деформацию сжатия – отрицательной. Продольная и поперечная деформации связаны соотношением

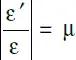
μ – коэффициент поперечной деформации, который имеет свое значение для разных тел (в пределах упругого деформирования). Этот коэффициент называют коэффициентом Пуассона.

В пределах упругого деформирования экспериментально была установлена прямая зависимость между нормальным напряжением σ и относительной деформацией ε .

σ = Eε

Это соотношение носит название закона Гука, а коэффициент пропорциональности E называется модулем упругостипервого рода. Модуль упругости – это величина, постоянная для каждого материала. Из соотношения видно, что при постоянном напряжении деформация меньше при большем модуле упругости.

Если рассматривать участок длиной l , на котором продольная сила и площадь поперечного сечения постоянны, закон Гука можно представить в виде:

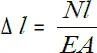
Произведение EA называется жесткостью сечения.

При растяжении или сжатии стержня его сечения перемещаются. Осевое перемещение сечений друг относительно друга равно изменению длины стержня между этими сечениями. График, на котором изображены перемещения всех сечений относительно одного, принятого за неподвижное, называется эпюром перемещений.