Роман Сиренко - Сопротивление материалов. Шпаргалка для студентов
- Название:Сопротивление материалов. Шпаргалка для студентов
- Автор:
- Жанр:
- Издательство:Научная книга
- Год:2009
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Роман Сиренко - Сопротивление материалов. Шпаргалка для студентов краткое содержание
Сопротивление материалов. Шпаргалка для студентов - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
∆ℓ RB= ∆ℓ t
Это и есть условие совместности деформаций; оно указывает на то, что при изменении температуры длина стержня не изменилась, он не оторвался от неподвижных опор. По закону Гука
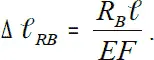
Приравнивая обе деформации, получаем:
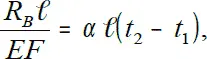
откуда R B= α×(t 2-t 1)×EF; 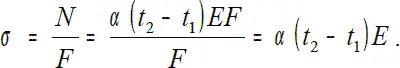
Напряжение, вызванное изменением температуры в стержне постоянного сечения с жестко защемленными концами, зависит лишь от материала, коэффициента линейного расширения, разности температур и не зависит от его длины и площади поперечного сечения.
9. Напряжения по наклонным сечениям при осевом растяжении и сжатии (линейное напряженное состояние)
Вычислим напряжения, действующие по какому-либо наклонному сечению. Возьмем призматический стержень, растянутый силами Р (Рис. 3.1).
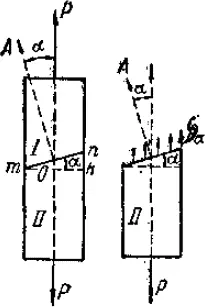
Рис. 3.1
Разделим его на две части сечением mn, составляющим угол α с поперечным сечением mk, перпендикулярным к оси. За положительное направление угла возьмем направление против часовой стрелки. Площадь сечения mk обозначим F 0, площадь сечения mn обозначим F α.Для определения напряжений применим метод сечений. Мысленно отбросим верхнюю часть и заменим ее действие на нижнюю напряжениями S α. Для равновесия нижней части напряжения S αдолжны уравновешивать силу Р и быть направлены параллельно оси стержня. Предполагая, как и раньше, что напряжения S αравномерно распределены по площади сечения, найдем: S α·F α= P, отсюда 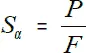 . Но, так как
. Но, так как 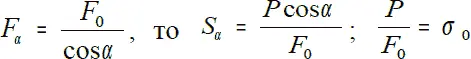 – нормальное напряжение по площадке mk, следовательно, S α=σ 0cosα. Для того чтобы при любом угле наклона α иметь дело с одними и теми же видами напряжений, разложим напряжение S αна две составляющие: в плоскости mn и перпендикулярно к ней (Рис. 3.2).
– нормальное напряжение по площадке mk, следовательно, S α=σ 0cosα. Для того чтобы при любом угле наклона α иметь дело с одними и теми же видами напряжений, разложим напряжение S αна две составляющие: в плоскости mn и перпендикулярно к ней (Рис. 3.2).
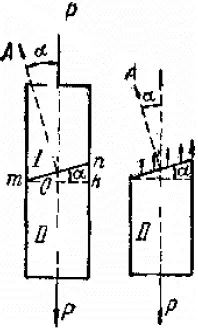
Рис. 3.2
Таким образом, напряжение S αзаменяем двумя взаимно перпендикулярными напряжениями: нормальным напряжением σ αи касательным напряжением τ α. Величины этих двух напряжений будут меняться в зависимости от изменения угла α между нормалью к площадке и направлением растягивающей силы.
Из Рис. 3.2 имеем:
σ α= S α·cosα = σ 0cos 2α;
τ α=S α· sinα = σ 0sinα · cosα = ½σ 0sin2α.
Принимаем правило знаков: растягивающие напряжения σ α, т. е. совпадающие с направлением внешней нормали, будем считать положительными; нормальные напряжения обратного направления – сжимающие – будем принимать со знаком минус. Касательное напряжение считается положительным, если оно дает момент по часовой стрелке относительно центра рассматриваемого сечения, отрицательным, если оно дает момент против часовой стрелки. Наличие этих двух видов напряжений соответствует наличию двух видов деформаций: продольной деформации и деформации сдвига. Для проверки прочности необходимо установить наибольшие значения σ αи τ αв зависимости от положения площадки mn. Из Рис. 3.2 понятно, что σ αдостигает своего наибольшего значения, когда cos 2α будет равен единице и угол α = 0. Максимум τ αполучится при sin 2α = 1, т. е. при 2α = 90° и α = 45°. Величины этих наибольших напряжений будут равны:
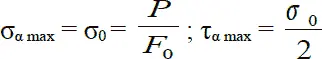
10. Понятие о главных напряжениях. Виды напряженного состояния материалов
Чтобы рассчитать прочность бруса при деформациях, нужно определить его напряжение в поперечном сечении. Если деформация сложная, то говорят о необходимости установить напряженное состояние в точке. Чтобы найти напряжение в точке, через эту точку нужно провести сечение. Через точку можно провести бесконечное множество сечений, следовательно, и напряжений в точке бесконечно много. Совокупность всех этих напряжений называется напряженным состоянием в точке.
Для нахождения напряженного состояния в точке тела возьмем элементарный параллелепипед с длинами сторон dx, dy, dz , при уменьшении этих длин сторон параллелепипед стягивается в точку. На грани этого параллелепипеда действуют напряжения, указанные на Рис. 4.1. (Имеется в виду, что указанные напряжения действуют на все грани). При поворотах параллелепипеда его напряжения изменяются, и можно подобрать такое положение, в котором все касательные напряжения будут равны нулю (Рис. 4.2). Площадки, на которых действуют только положительные напряжения, называют главными, соответственно, нормальные напряжения на этих площадках также называются г лавнымии обозначают σ 1, σ 2, σ 3. Наибольшее из напряжений обозначается σ 1, наименьшее – σ 3. Необходимо учитывать знаки: напряжения растяжений считаются положительными, напряжения сжатия – отрицательными. Если известны напряжения на трех взаимно перпендикулярных площадках, то напряжение в точке тоже считается известным.
Главные напряжения могут быть как положительными, так и отрицательными и действовать по всем направлениям координатных осей.
Если напряжение действует только в направлении одной из осей, то оно называется одноосным или линейным.
Если напряжение действует в двух направлениях, то оно называется двухосным, или плоским.
Если напряжение действует по всем направлениям координатной оси, то такое напряжение называют трехосным, или объемным.
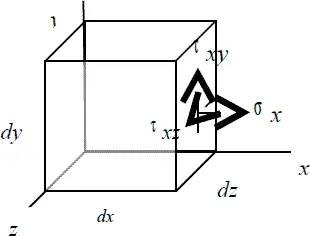
Рис. 4.1
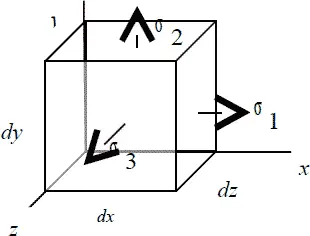
Рис. 4.2
11. Плосконапряженное состояние материалов
В сопротивлении материалов чаще всего встречаются задачи, когда напряжение действует в двух направлениях, т. е. является плоским. Рассмотрим такое состояние.
Возьмем произвольную точку тела и рассмотрим элементарный параллелепипед с длинами сторон dx, dy, dz в ее окрестности. Рассечем этот параллелепипед плоскостью, перпендикулярной плоскости zy (Рис. 5.1).
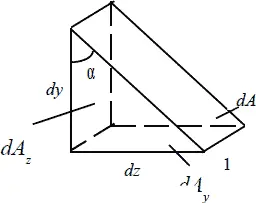
Рис. 5.1
Читать дальшеИнтервал:
Закладка:








