Роман Сиренко - Сопротивление материалов. Шпаргалка для студентов
- Название:Сопротивление материалов. Шпаргалка для студентов
- Автор:
- Жанр:
- Издательство:Научная книга
- Год:2009
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Роман Сиренко - Сопротивление материалов. Шпаргалка для студентов краткое содержание
Сопротивление материалов. Шпаргалка для студентов - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
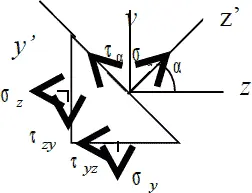
Рис. 5.2
На Рис. 5.2 изображены напряжения на поверхности полученной призмы. Из условий равновесия треугольной призмы через проекции сил, действующих на грани, на оси y’ и z’ , можно найти напряжения на наклонной грани призмы.
s α dA – σ z dA z cosα – σ ydA y sinα – τ zydA z sinα – τ yzdA y cosα = 0
τ α dA + σ zdA z sinα – σ ydA y cosα – τ zydA z cosα + τ yzdA y sinα = 0
Учитывая, что dA z = 1 dy = dA cosα, dA y = 1 dz = dA sinα, записанные отношения в результате тригонометрических преобразований примут вид:
σ α= σ z cos 2α + σ y sin 2α + τ zy sin2α
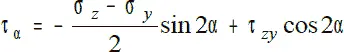
Если совместить оси координат z, y c направлениями главных напряжений, то соотношения примут вид:
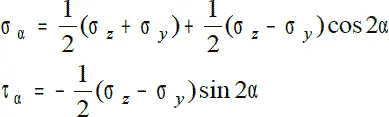
Из последнего уравнения следует, что при α = 45° касательные выражения принимают свои экстремальные значенияв точке.
τ max= ½(σ z – σ y )
Частный случай плоского напряженного состояния: при σ x = σ y τ α=0, на всех проведенных через точку площадках касательные напряжения равны нулю, т. е. все площадки – главные с нормальными напряжениями σ α= σ y = σ z = σ. Примером такого состояния может служить стенка воздушного шара, находящаяся под давлением.
При σ x = – σ y = σ на грани элемента действуют численно равные сжимающие и растягивающие напряжения. Экстремальные касательные напряжения равны главным, а нормальные напряжения равны нулю. Такой частный случай носит название чистого сдвига.
12. Графическое определение напряжений (круг Мора)
По известным напряжениям, действующим на площадках, взаимно перпендикулярных друг другу и проходящих через заданную точку, можно определять напряжения по другим площадкам. Это осуществляется графическим способом, который был предложен немецким физиком О. Мором.
Запишем формулы для определения нормальных и касательных напряжений для площадок, проходящих через заданную точку, в виде:
σ = σ x cos 2α + σ y sin 2α + τ x sin2α
τ = (σ x – σ y )sin2α – τ x cos2α
Преобразуем первое выражение:
σ = ½σ x (1 + cos2α) + ½σ y (1 – cos2α) + τ x sin2α
После тригонометрических преобразований формулы для напряжений запишутся в виде:
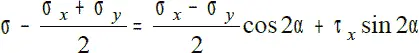
τ = (σ x – σ y )sin2α – τ x cos2α
Обе части этих выражений возведем в квадрат, а затем сложим:
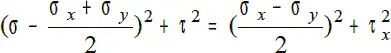
Сопоставим полученное 2 уравнением окружности ( x – a ) 2+ ( y – b ) 2= R 2.
Будем считать ось абсцисс осью нормальных напряжений, а ось ординат – осью касательных напряжений, график зависимости между этими напряжениями представляет окружность, центр которой находится в точке с координатами 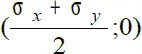 и радиусом, определяемым формулой
и радиусом, определяемым формулой 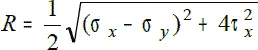 . График этой окружности называется кругом напряжений, или кругом Мора.
. График этой окружности называется кругом напряжений, или кругом Мора.
Пример напряженного состояния и построенного для него круга Мора приведен на Рис. 6.1. Координаты каждой точки этого графика представляют собой напряжения по одной из площадок, проходящих через точку тела, для которой построен график напряженности.
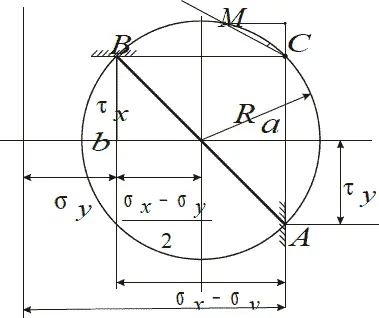
Рис. 6.1
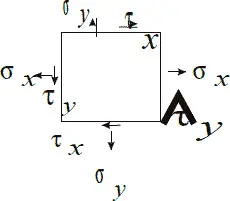
Рис. 6.2
При помощи круга Мора также определяются главные напряжения и положения главных площадок (Рис. 6.2), а также экстремальные касательные напряжения.
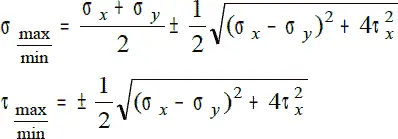
13. Объемно-напряженное состояние материала
Для изучения объемно-напряженного состояния материала выберем произвольную точку тела, находящегося в напряженном состоянии, и выделим в окрестности этой точки элементарный кубик, по граням которого действуют главные напряжения σ 1, σ 2, σ 3.
Проведем сечения, параллельные каждому из главных напряжений, и определим значение нормальных и касательных напряжений на этих площадках (Рис 7.1, Рис. 7.2, Рис. 7.3).
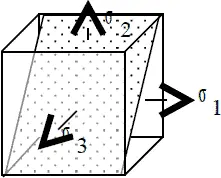
Рис. 7.1
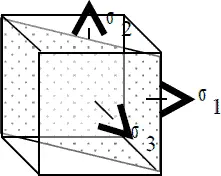
Рис. 7.2
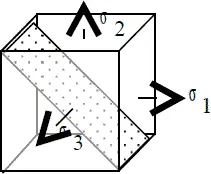
Рис. 7.3
Из условий равновесий составленных для отсеченных участков кубиков следует, что действующие на наклонных площадках напряжения не зависят от того из главных напряжений, параллельно которому эти площадки проведены. Обозначим угол наклона площадки α, применив принцип независимости действия сил, нормальные и касательные напряжения рассмотрим как сумму действия напряжений от σ 1и σ 2.
σ α= σ 1cos 2α + σ 2cos 2(α + 90°)
τ α= 0,5σ 1sin2α + 0,5σ 2sin2(α + 90°)
Выполнив математические преобразования, запишем соотношения в виде:
σ α= σ 1cos 2α + σ 2sin 2α
τ α= 0,5(σ 1+ σ 2)sin2α
Полученные формулы определяют нормальные и касательные напряжения в случае объемно-напряженного состояния материала, они же соответствуют двухосному плоско-напряженному состоянию.
Максимальное касательное напряжение при объемном напряженном состоянии материала существует на площадке, параллельной напряжениюσ 2 , нормаль к площадке составляет угол в 45° и определяется по формуле:
τ max= 0,5(σ 1– σ 3)
14. Деформации при плоском и объемном напряженных состояниях (обобщенный закон Гука)
В пределах упругого деформирования была установлена прямая зависимость между нормальным напряжением σ и относительной деформацией ε, носящая название закона Гука.
σ = E e
Для нахождения деформации нужно выбрать одну из точек исследуемого тела и мысленно рассмотреть элементарный кубик в ее окрестности, на который действуют главные напряжения. Деформация кубика происходит во всех трех направлениях главных напряжений σ 1, σ 2, σ 3. Такие деформации называются главными деформациямии обозначаются ε 1, ε 2, ε 3. Совокупность главных деформаций в точке тела определяет деформированное состояние в точке.
Читать дальшеИнтервал:
Закладка:








