Роман Сиренко - Сопротивление материалов. Шпаргалка для студентов

Чтобы определить главные деформации объемного напряженного состояния, сначала определим деформации, связанные с отдельными главными напряжениями и сложим результаты. Деформация ε 1напряжения σ 1в том же направлении, что и σ 1из закона Гука равна:

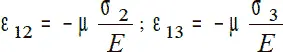
Тогда деформация от всех главных напряжений в направлении σ 1

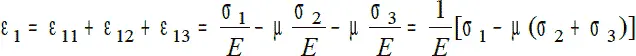
Таким же образом определяются деформации в направлении других главных напряжений.

В результате получим следующую систему уравнений, представляющую собой закон Гука в общем виде:

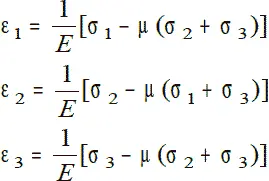
Эти уравнения можно записать для линейного и плоского напряженного состояния материалов, если убрать соответствующие слагаемые.

Из полученной системы уравнений видно, что, зная главные напряжения, можно найти напряженное и деформированное состояния в точке, причем эти состояния могут не совпадать.

При возникновении деформации внешние силы совершают работу, связанную со смещением точек приложения этой силы. Элементарная работа dA внешней силы F определяется по формуле:

dA = Fdl’

где dl’ – перемещение точки приложения силы.

Из закона Гука известно:

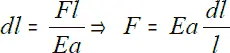
В этом соотношении l – длина рассматриваемого участка до деформации;

dl – изменение длины;

a – площадь поперечного сечения тела.

Таким образом,

dA = Eadl’dl / l

Проинтегрировав полученное равенство от нуля до окончательного значения перемещения l’ , найдем полную работу силы.

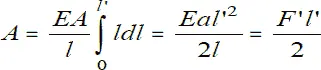
При воздействии на тело внешних статических сил работа этих сил определяется как половина произведения окончательного значения силы на конечное значение перемещения точки приложения этой силы.

A = F’l’ / 2

При воздействии на тело постоянных внешних сил работа этих сил определяется как произведение значения этой силы на конечное значение перемещения точки приложения этой силы.

A = F’l’

Внутренние силы направлены противоположно перемещению, поэтому считается, что работа внутренних сил при нагружении отрицательна. Элементарная работа внутренних сил рассчитывается аналогично работе внешних сил.

dA вн = Ndl / 2

где N – продольная сила (внутренне усилие).

Вновь воспользовавшись законом Гука, имеем:

dA вн = – N 2 dl / 2 Еa

Интегрируя соотношение по длине рассматриваемого участка, получим полную работу внутренних сил:

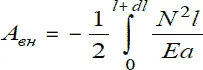
Потенциальной энергией деформации называется величина, равная модулю работы внутренних сил, онапредставляет собой энергию, которая накапливается телом при деформации.

U = Eal 2/ 2( l + dl )

При расчетах различных конструкций и сооружений в случае деформации широко используются свойства механической энергии.

Если под воздействием нагрузки тело переходит в деформированное состояние, то сумма работ внутренних и внешних сил равна нулю. Это свойство энергии носит название закона сохранения механической энергии.

Действительное напряженное состояние равновесия упругого тела отличается от всех других состояний тем, что в этом состоянии потенциальная энергия деформации минимальна. Это свойство справедливо для тел, подчиняющихся закону Гука, и называется принципом наименьшей работы.

При неограниченном нагружении материал конструкции или сооружения проходит несколько стадий своего состояния:

– упругую стадию, когда в материале под воздействием небольших нагрузок происходят упругие деформации;

– пластическую стадию, когда под влиянием увеличивающейся нагрузки в материале происходят пластические деформации;

– стадию разрушения, когда под воздействием больших нагрузок тело покрывается трещинами.

В случаях линейного напряженного состояния проверка на прочность довольно проста и осуществляется путем растяжения (сжатия). В случае сложного напряженного состояния (плоскостного или объемного) количество вариантов напряженных состояний велико, и опытным путем осуществить проверку практически невозможно. Для оценки прочности при сложном напряженном состоянии используют гипотезы прочности, которые проводить расчеты на прочность по известным характеристикам прочности. Наиболее широко используются три гипотезы, кратко рассмотрим их.

Гипотеза максимальных касательных напряжений:два напряженных состояния считаются равноопасными в том случае, если максимальные касательные напряжения для них равны. Предполагается, что сложное напряженное состояние можно заменить равноопасным одноосным растяжением с условием, что максимальные касательные напряжения для них равны.

Для пластичных материалов, у которых характеристики прочности одинаковы при растяжении и сжатии, эта теория хорошо подтверждается. Условие прочности записывается в виде:

σ экв = σ 1– σ 3≤ [σ p ]

Если известны не главные напряжения, а нормальное и касательные напряжения в поперечном сечении, условие прочности имеет вид:

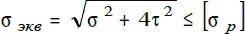
Энергетическая гипотеза прочности:два напряженных состояния равноопасны, если их равны их удельные потенциальные энергии формоизменения. Эта гипотеза предполагает замену сложного напряженного состояния эквивалентным одноосным напряжением при условии равенства их удельных потенциальных энергий формоизменения.

Для пластичных материалов, у которых характеристики прочности одинаковы при растяжении и сжатии, эта теория хорошо подтверждается. Ее преимущество перед гипотезой максимальных касательных напряжений состоит в том, что она включает все три главных напряжения.

Условие прочности, если известны главные напряжения, выглядит следующим образом: