Владимир Живетин - Научный риск (введение в анализ)
- Название:Научный риск (введение в анализ)
- Автор:
- Жанр:
- Издательство:Институт проблем риска, ООО Информационно-издательский центр «Бон Анца»
- Год:2008
- Город:Москва
- ISBN:978-5-98664-040-2, 978-5-903140-16-9
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Владимир Живетин - Научный риск (введение в анализ) краткое содержание
Научный риск (введение в анализ) - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
В математике, где главным и определяющим фактором достоверности выступает человеческий фактор [24], так же, как и в других науках, возникают неопределенности, ошибки, которые приводят к ложным выводам. В математической энциклопедии дано следующее определение доказательства: «Доказательство – рассуждение по определенным правилам, обосновывающее какое-либо предположение (утверждение, теорему); основанием доказательства служат исходные утверждения (аксиомы)… Всякое доказательство относительно, поскольку базируется на некоторых недоказуемых положениях».
В математике, для которой характерен аксиоматический метод исследования, средства доказательства достаточно четко определились на раннем этапе ее развития. При этом используется последовательное выведение одних суждений из других, причем способы выведения допускают точный анализ. Отметим, что начало дедуктивного метода доказательства в элементарной геометрии, силлогистике было заложено Аристотелем.
Предположим, что при исследовании некоторых свойств абстрактного объекта создана система понятий и аксиом. При этом возможны следующие ситуации: оцениваются одна теория, ее непротиворечивость и достоверность; оцениваются две теории по одному суждению. При этом необходимо выяснить непротиворечивость данной системы понятий и аксиом для того, чтобы гарантировать истинность доказанных в ней ситуаций.
Непротиворечивость – достаточно сложная проблема. Так, Гёдель доказал, что утверждение о непротиворечивости данной формальной системы в рамках самой системы недоказуемо, если она непротиворечива. Гильберт писал: «Подумайте: в математике, этом образце достоверности и истинности, образование понятий и ход умозаключений… приводят к нелепостям. Где же искать надежность и истинность, если даже само математическое мышление дает осечку?». В продолжение этого: «Развитие теории познания показало, что никакая форма умозаключения не может дать абсолютно достоверного знания» [2].
Иногда доказанное суждение представляет собой относительную истину, т. е. включает в себя не только достоверные, но и недостоверные знания. Так, например, применимость данной логики к одному кругу объектов из области G еще не означает возможность применимости ее в более широкой области G 1: G 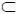 G 1. При этом сформулированные для доказательства понятия и определения, аксиомы приводят к противоречию при доказательствах существования объектов в другой области со сформулированными свойствами. Так, при исследовании динамических объектов (систем) возникает необходимость изучать их траектории, представляющие собой случайные процессы. В теории случайных процессов, как правило, свойства конкретных физических объектов не учитываются. Здесь рассматривается абстрактный объект, которому ставят в соответствие абстрактный случайный процесс, например марковский, для которого имеется большое количество глубоких результатов. Так, для марковских процессов можно построить уравнение Фоккера – Планка – Колмогорова, с помощью которого можно рассчитать чрезвычайно важное свойство случайного процесса – переходную плотность вероятностей. Для этих же процессов, выступающих в роли абстрактных объектов, строятся модели достижения границ и т. д. Такие модели, как правило, не отражают физический мир, такие процессы могут быть и не порождены реальностью, а самое важное – в том, что нас не интересует их первопричина: они сами, оторванные от физического мира, суть объект исследования, первопричина.
G 1. При этом сформулированные для доказательства понятия и определения, аксиомы приводят к противоречию при доказательствах существования объектов в другой области со сформулированными свойствами. Так, при исследовании динамических объектов (систем) возникает необходимость изучать их траектории, представляющие собой случайные процессы. В теории случайных процессов, как правило, свойства конкретных физических объектов не учитываются. Здесь рассматривается абстрактный объект, которому ставят в соответствие абстрактный случайный процесс, например марковский, для которого имеется большое количество глубоких результатов. Так, для марковских процессов можно построить уравнение Фоккера – Планка – Колмогорова, с помощью которого можно рассчитать чрезвычайно важное свойство случайного процесса – переходную плотность вероятностей. Для этих же процессов, выступающих в роли абстрактных объектов, строятся модели достижения границ и т. д. Такие модели, как правило, не отражают физический мир, такие процессы могут быть и не порождены реальностью, а самое важное – в том, что нас не интересует их первопричина: они сами, оторванные от физического мира, суть объект исследования, первопричина.
В качестве примеров взаимного проникновения различных теорий, обогативших методы изучения абстрактных объектов, можно рассмотреть: использование теории случайных процессов для исследования объектов математической физики [20]; исследование вероятностных объектов с помощью теории потенциалов [43].
В настоящее время существуют глубокие и хорошо разработанные связи между уравнениями математической физики и случайными процессами, суть которых была открыта в 20-х годах прошлого столетия в работах Н. Винера, Р. Куранта, К. Фридриха и Х. Леви. Все эти работы обусловили введение нового математического объекта – интеграла по траекториям случайного процесса, а также более общего объекта – континуального интеграла, который играет важную роль в современной математической физике. Эти объекты используются в квантовой механике (интеграл Фейнмана), в классической статистической физике и в ряде областей математики, что обусловило необходимость разработки эффективных средств их приближенного вычисления.
Одним из таких методов является метод Монте-Карло, позволяющий моделировать марковские процессы и интегралы по траекториям более общего характера. Недостатком метода принято считать скорость убывания его погрешности, которая в случае конечности второго момента используемой оценки ведет себя как О ( N –1/2), где N – число моделируемых траекторий. Учет априорной информации относительно решения задачи позволяет уменьшить константу при N –1/2, что позволит комбинировать этот метод с другими и использовать приближенные решения при более грубых предположениях.
Глава II. Мировоззрение как развивающаяся система
2.1. Становление знания
Становление знания человека обусловлено появлением душевной энергетики, направленной на защиту тела от воздействий агрессивной окружающей среды, на приобретение навыков по обеспечению жизни, на осмысление своих действий. При этом в процессе жизнедеятельности сформировались знания конкретного человека, общины, сообщества, объем V 3которых можно представить в виде
V 3= V 3( П, Р, Ф, Н, W ), (2.1)
где П – практика, включающая знания, полученные в процессе практической деятельности, профессиональные знания (чувственный опыт); Р – религия, знания которой получены в процессе религиозной деятельности, духовного осмысления среды жизнедеятельности (религиозный опыт); Ф – философия, где знания, полученные философами, созданы на стыке религии, практики, а впоследствии и науки; Н – наука, научные знания, полученные на базе религиозных, философских и практических изысканий; W – неопределенные, возмущающие факторы как внутренние, так и внешние по отношению к изучаемым объектам.
В простейшем случае (приближенно) (2.1) можно записать в виде
V 3= K 1 П + K 2 P + K 3 Ф + K 4 H + K 5 W , (2.2)
где K i – коэффициенты, переменные во времени, т. е. K i = K i ( t ), 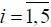 .
.
Интервал:
Закладка:










