Виктор Шаповалов - Моделирование синергетических систем. Метод пропорций и другие математические методы. Монография

Таким образом, в экономически развитых регионах α и γ должны иметь сравнительно большие значения, а β – малое. Поэтому β 2 – 4 αγ < 0, т. е. в выражении для k 1,2разность под корнем имеет отрицательный знак. Следовательно, k 1,2– комплексные:

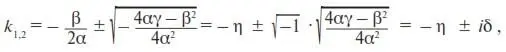
где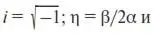

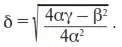(8)

Как видим, k 1,2соответствуют 4-му типу решения ОЛУ (см. Приложение, раздел П1.3). В этом случае решением уравнения (7) является выражение

y* = е – ηt (A 1cos δt + A 2sin δt) , (9)

где A 1и A 2− константы интегрирования.

Частное решение y 1определим по виду правой части уравнения, в качестве которой в (5) выступает a/α . Последнее соответствует первому виду правой части НОЛУ (см. Приложение, раздел П1.4), а именно

f (t) = p (t) e γt . (10)

Действительно, для уравнения (5) функцию f ( t ) можно записать как

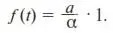(11)

Сравнивая между собой (10) и (11), находим, что в нашей задаче

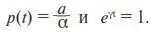(12)

Напомним, что число, возведенное в степень, равно единице только в том случае, если степень равна нулю. Следовательно, γ = 0. Как видим, γ не совпадает с корнями характеристического уравнения k 1,2. Поэтому для y 1выбираем первый тип решения (выбираем пункт 1.аиз раздела П1.4 Приложения):

y 1= q(t) e γt = q(t)

( e γt = 1, см. (12)). Определим вид q ( t ). Для этого учтем, что: а) q ( t ) – многочлен той же степени, что и р ( t ); б) в нашем случае р ( t ) – многочлен нулевой степени:

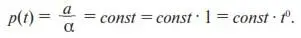
Следовательно, и q(t) является многочленом нулевой степени, т. е. является постоянной величиной. Обозначим эту постоянную, например, с: q(t) = c . Тогда

y 1= q(t) = c. (13)

Постоянную с найдем, подставив y 1 в (5):

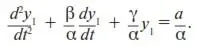
Воспользуемся (13):

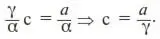
Здесь мы учли, что

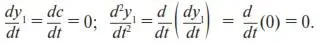
Найденное значение с подставим в (13):

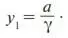
– частное решение уравнения (5). Его общее решение запишем по формуле (6) ( y * возьмем из (9)):

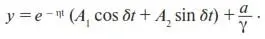(14)

Выражение в скобках можно упростить, заменив постоянные A 1и A 2на новые постоянные A и φ 0по формулам

A 1= A sin φ 0и A 2= A cos φ 0

(легко увидеть, что 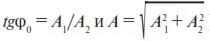). Тогда

A 1cos δt + A 2sin δt = A (sin φ 0cos δt + cos φ 0sin δt) = A sin (δt + φ 0).

В результате (14) примет вид

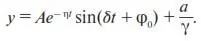(15)

Уравнение (15) представляет собой формулу зависимости от времени количества товара, приобретаемого благодаря действию рекламы.

Из (15) следует, что если рекламировать товар с постоянной интенсивностью достаточно долго ( a = const ), то начнутся колебания y вокруг постоянного значения a/γ , т. е. возникнет чередование периодов положительного и отрицательного восприятия рекламы (см. рис. 1).

Сравним (15) с известным законом колебательного движения

x = A sin (ωt + φ 0).

Как видим, δ совпадает по смыслу с циклической частотой ω . Отсюда, воспользовавшись соотношением для периода колебаний T = 2π/ω , получаем формулу для промежутка времени положительного восприятия рекламы:

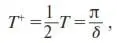
где δ вычисляется из (8). Для определения численных значений коэффициентов, входящих в (8), возможно использование эконометрических методов.

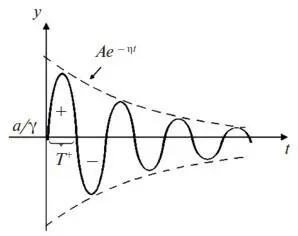
Рис. 1.Чередование периодов положительного и отрицательного восприятия рекламы

К настоящему времени в экономике системные закономерности наиболее подробно рассмотрены в математических моделях экономического роста крупных регионов, например городов, областей, государств (см., например, [7,14]). При этом в качестве переменных величин, как правило, выбирались национальный доход, капитал, средний уровень зарплаты, цены и т. п. Модели таких систем характеризуют результаты согласованного поведения большого количества фирм, входящих в регион. В данной главе будет проведен анализ поведения отдельной фирмы, для которой экономика региона играет роль внешней среды.

Мы рассмотрим фирму, обладающую следующими средними (по региону) показателями: числом сотрудников и величиной оборотного капитала. Главная задача данного раздела – раскрыть важную роль управляющих параметров, которую они играют при выборе системой пути к тому или иному устойчивому состоянию.

Вначале мы построим общую математическую модель поведения средней фирмы. Затем в качестве примера найдем устойчивые состояния предприятия, занимающегося конкретным видом деятельности, например страхованием.

(Изложение данного раздела следует работам [26, 28].) Пусть в фирме работает Y 1сотрудников, а ее капитал, выраженный в некоторых условных единицах, равняется Y 2. Необходимо определить, возможно ли в такой системе устойчивое состояние и какому типу устойчивости оно соответствует?