Виктор Шаповалов - Моделирование синергетических систем. Метод пропорций и другие математические методы. Монография

Эволюционная диаграмма переменной Y 1показана на рис. 4. Штриховой линией обозначены фазовые траектории в пространстве Y 1, Y 2. Огибающие этих траекторий выделены. Вид сечения эволюционной диаграммы в месте сшивки двух конусов в координатах Y 1и Y 2совпадает с предельным циклом. При этом очевидно, что радиус спирали с течением времени стремится к значению √ ε по оси Y 1. Причем если речь идет о малом значении ε , т. е. о малой вязкости γ 0, то вид устойчивого стационарного решения закона (35) должен быть близок к уравнению окружности [2]:

Y 2 1ст+ Y 2 2ст≈ ε .

2.3.4.Таким образом, в фазовом пространстве двух переменных генератору Ван дер Поля соответствует устойчивая замкнутая траектория (аттрактор) – предельный цикл.

Сравнивая между собой эволюционные диаграммы, представленные на рис. 2 и 4, приходим к выводу об общих закономерностях возникновения устойчивых состояний описанных экономической и физической систем.

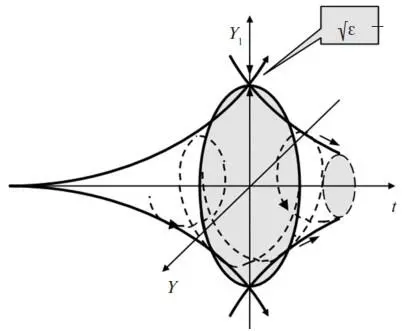
Рис. 4

Различные системы по разным причинам попадают в неустойчивое состояние. Однако, попав в него, они подчиняются общим закономерностям, отражающим суть неустойчивого состояния. При этом бифуркационные закономерности занимают среди названных не последнее место (о бифуркациях см. Приложение, раздел П5).

Биологические системы – это открытые и неравновесные системы. Достигнуть равновесия им постоянно мешает какое-нибудь внешнее воздействие. В математическом отношении внешнее воздействие учитывается с помощью управляющего параметра в эволюционном уравнении. Если изменяются внешние условия, то изменяется и величина управляющего параметра. Последнее же, как мы видели, приводит к смене типов устойчивости. В результате при определенном значении этого параметра система может оказаться неустойчивой и, следовательно, подверженной бифуркации.

Чаще всего бифуркация – это единственный выход для системы из неустойчивого состояния. Другим выходом, разумеется, является обратный ход по значениям управляющего параметра, однако для этого придется изменять внешние условия (также в обратную сторону), что по силам далеко не каждой системе. Кроме того, бифуркация дает новые состояния и поэтому лежит в основе прогрессивного развития природы. В частности, многие (если не все) биологические виды своим появлением обязаны именно бифуркационным процессам в природе. Задача, рассмотренная в настоящем разделе, в какой-то мере поможет понять некоторые детали этого явления.

Итак, имеется система, состоящая из микроорганизмов размножающихся путем деления. Эта система находится в среде с начальной массой пищи m 0. Требуется исследовать бифуркационное поведение данной системы, т. е. построить бифуркационную диаграмму и определить точки бифуркации.

Если масса пищи m не регулируется извне, то закон ее убывания с ростом числа микроорганизмов близок к экспоненциальному (см., например, [11]):

m = m 0exp(—βn) ,

где n = N/V – концентрация микроорганизмов; N – число микроорганизмов; V – объем среды; β – коэффициент потребления , показывающий, как быстро с ростом n уменьшается пища.

Скорость размножения dn/dt пропорциональна концентрации уже имеющихся микроорганизмов и массе пищи, следовательно [11],

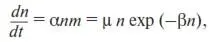(40)

где µ = αm 0, α – коэффициент пропорциональности, характеризующий благоприятные условия среды обитания (благоприятные потому, что, как видно из (40), чем больше α , тем больше dn/d t – прирост числа микроорганизмов).

Учтем смертность микроорганизмов. Для этого воспользуемся следующими соображениями: с одной стороны, с ростом числа умерших скорость появления новых микроорганизмов падает, а с другой стороны, число умерших микроорганизмов пропорционально числу имеющихся. Поэтому в (40) из правой части нужно вычесть величину, пропорциональную n :

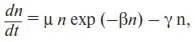(41)

где γ – коэффициент, показывающий, какую долю от общего числа микроорганизмов составляют умершие. Другими словами, коэффициент γ отражает факторы, способствующие увеличению смертности, т. е. этот коэффициент характеризует неблагоприятные условия среды обитания.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.