Виктор Шаповалов - Моделирование синергетических систем. Метод пропорций и другие математические методы. Монография

Коэффициент γ характеризует долю клиентов, решивших расторгнуть страховые отношения с данной фирмой (см. формулировку первой главной пропорции в 2.2.2.1). Если фирма не банкрот, то γ должна быть малой величиной.

Напомним, что σ = β/p , при этом p – размер страховой выплаты клиенту, т. е. большая величина. Поэтому мы полагаем σ малой величиной.

Так как η = s β/p , т. е. в s раз больше, чем σ, то η полагаем сравнительно большой величиной (напомним, что s >>1).

Величина c также должна быть большой, так как этот коэффициент пропорционален доходу D 0( D 0> 1) и количеству несчастных случаев Q за некоторый период ( Q >> 1).

В результате получаем следующее распределение знаков:

B > 0; ∆ < 0; D > 0.

Такое сочетание знаков совпадает с (П32). В этом случае стационарное решение (28) соответствует седловой неустойчивости.

Таким образом, решение (28) является неустойчивым.

2. Проверим на устойчивость стационарное состояние (29). Для этого его стационарные значения Y 1сти Y 2стподставим в (32) и (33). В результате с учетом (30) и (31) найдем:

a 11= – γ; a 12= c;

a 21= µY 2ст– η = 0 – η = – η;

a 22= µY 1ст+ σ = 0 + σ = σ.

По формулам (П22) вычислим B , ∆ и D :

B = σ – γ, ∆ = ηc – σγ, D = (σ + γ) 2– 4ηc.

Выше мы уже установили, что γ и σ меньше, чем η и с . Это позволяет нам определить знаки только величин ∆ и D : ∆ > 0; D < 0. Для B возникают две ситуации.

Ситуация 1: σ > γ . В этой ситуации большинство клиентов сохраняют верность фирме ( γ уменьшается). При этом распределение знаков имеет вид

B > 0; ∆ < 0; D > 0.

Последнее совпадает с (П30), т. е. в данном случае решение (29) соответствует неустойчивому фокусу (см. рис. П5). Расширяющаяся спираль указывает на рост значений переменных Y 1и Y 2(числа клиентов и прибыли).

Ситуация 2: σ < γ. Эта ситуация возникает, если фирма по каким-либо причинам теряет часть клиентов ( γ увеличивается). Распределение знаков имеет вид

B < 0; ∆ < 0; D > 0.

Данное сочетание знаков совпадает с (П25), т. е. в данном случае решение (29) соответствует устойчивому фокусу (см. рис. П2). Сжимающаяся спираль указывает на уменьшение числа клиентов Y 1и прибыли Y 2.

На практике механизм перехода фирмы из одной ситуации в другую может выглядеть следующим образом.

В ситуации 1 благодаря состоянию «неустойчивый фокус» (расширяющаяся спираль в пространстве координат Y 1и Y 2) происходит рост числа клиентов и прибыли. По мере роста числа клиентов увеличивается и число страховых выплат. Наступает момент, когда клиентов становится настолько много, что их взносы не покрывают убыток от страховых выплат. В этом случае фирма вынуждена уменьшить, например, размер страховой премии. Из-за этого часть клиентов уходит из данной фирмы ( γ увеличивается). В результате фирма оказывается в ситуации 2. Этой ситуации соответствует состояние «устойчивый фокус» (сжимающаяся спираль в пространстве координат Y 1и Y 2). В таком состоянии число клиентов уменьшается до тех пор, пока прибыль фирмы не позволит вернуться к прежней повышенной страховой премии. В этом случае клиенты перестанут уходить из фирмы, что соответствует уменьшению γ . В результате фирма переходит в ситуацию 1, и т. д.

2.2.2.4.Таким образом, мы показали, что система «частная страховая фирма» с течением времени приходит к устойчивому состоянию, представляющему собой колебания вокруг оптимальных значений числа клиентов и размера прибыли. Сами оптимальные значения зависят от величин коэффициентов γ, σ, η и с .

В этом разделе мы покажем, что устойчивое поведение маятника, колеблющегося в среде с переменной вязкостью, и устойчивое поведение средней фирмы, рассмотренное нами в разделе 2.1, имеют много общего [28].

2.3.1.Рассмотрим систему, представляющую собой математический маятник, совершающий колебания в вязкой среде, коэффициент вязкости γ которой зависит от θ – угла отклонения маятника от положения равновесия – по следующему закону: а) γ < 0 при малых θ и б) γ > 0 при больших θ . Такая система при некотором критическом значении угла θ должна совершать устойчивые колебания по типу предельного цикла (т. е. с постоянной амплитудой) [2].

Нетрудно сообразить, что указанному закону удовлетворяет следующее выражение

γ = γ 0(θ 2– 1),

где γ 0– коэффициент вязкости среды в отсутствие колебаний.

Подставив это выражение вместо коэффициента вязкости в известное уравнение колебаний маятника в вязкой среде (см., например, (П15)), получим

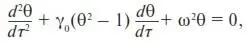(34)

где τ – время; ω 2= gK – квадрат циклической частоты колебаний; K – кривизна траектории маятника; g – ускорение свободного падения.

Уравнение (34) называется уравнением Ван дер Поля , а система, которую оно описывает, – генератором Ван дер Поля [2].

В безразмерном виде уравнение (35) имеет вид:

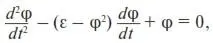(35)

где

2.3.2.Покажем, что устойчивым стационарным состоянием (аттрактором) генератора Ван дер Поля действительно является предельный цикл. С этой целью уравнение (35) приведем к виду эволюционного уравнения (см. (П6)):

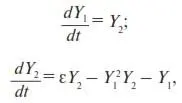
где Y 1= φ; Y 2= dφ/dt ;

F 1= Y 2;

F 2= εY 2– Y 1 2Y 2– Y 1. (36)

Находим стационарное решение

Y 1cm= Y 2ст= 0. (37)

По формуле (П12) с учетом (36) находим коэффициенты линейного разложения

а 11= 0;

а 12= 1;

а 21= –2Y 1стY 2ст– 1;

а 22= ε – Y 21ст.

По формулам (П22) находим

B = ε – Y 2 1ст;

∆ = 2Y 1стY 2ст+ 1; (38)

D = (ε – Y 2 1ст) 2– 4 ∆.

Подставив стационарное решение (37) в (38), получим, что

B > 0; ∆ > 0; D = ε 2– 4. (39)

2.3.3.Если ε достаточно мало, то D становится отрицательным, а распределение знаков в (39) соответствует неустойчивому фокусу (см. (П30)). В этом случае фазовая траектория в координатах Y 1и Y 2будет представлять собой спираль, раскручивающуюся из начала координат (см. рис. П5).

Раскручивание спирали приводит к тому, что с течением времени увеличивается переменная Y 1, которую мы использовали для обозначения угловой величины φ из уравнения (35). Если величина φ вырастает настолько, что выполняется φ 2> ε , то знак перед производной первого порядка в уравнении (35) становится положительным. Тогда в первом из уравнений (38) мы получим, что B = — ε (при Y 1cm= 0), т. е. B < 0. Учитывая, что ∆ > 0; D < 0, и сравнивая с выражением (П25), приходим к заключению о том, что в этом случае стационарное решение (37) является устойчивым фокусом. Фазовая траектория представляет собой спираль, сходящуюся к началу координат (см. рис. П2).