Виктор Шаповалов - Моделирование синергетических систем. Метод пропорций и другие математические методы. Монография

Поиск устойчивых стационарных состояний проведем с помощью линейного анализа устойчивости. Для этого воспользуемся его схемой (см. Приложение П2.2).

2.1.1.Начнем с составления эволюционного уравнения. Левая часть эволюционного уравнения представляет собой производные первого порядка от величин, принятых в качестве переменных (см. (П6) 3). В нашем случае речь идет о Y 1и Y 2:

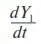– скорость роста числа сотрудников;

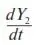– скорость увеличения капитала фирмы.

Сформулируем первую главную пропорцию 4:

скорость роста числа сотрудников ( dY 1/ dt ) пропорциональна числу новых сотрудников минус ту ее часть, которая связана с количеством уволившихся.

При этом количество новых сотрудников пропорционально капиталу фирмы (~ Y 2, так как в среднем люди предпочитают работать в более богатой фирме), а количество уволившихся составляет некоторую долю от числа имеющихся (~ Y 1). Заменяя знаки пропорции (~) на коэффициенты пропорциональности, первую главную пропорцию приводим к следующему уравнению:

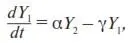(16)

где α – коэффициент пропорциональности, показывающий, какую часть своего капитала может выделить фирма, чтобы привлечь новых сотрудников; γ – коэффициент пропорциональности, обобщающий в себе различные причины, в результате которых сотрудник может уволиться (или его уволят).

Cформулируем вторую главную пропорцию:

скорость увеличения капитала пропорциональна прибыли от вложения капитала минус расходы на сотрудников.

При этом прибыль от вложения капитала пропорциональна величине вложенного капитала (~ Y 2), а расходы на сотрудников пропорциональны их количеству (~ Y 1). Так же заменяя знаки пропорции (~) на коэффициенты пропорциональности, вторую главную пропорцию приводим к уравнению:

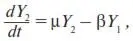(17)

где µ – коэффициент пропорциональности, показывающий эффективность работы фирмы на рынке; β – коэффициент пропорциональности, обобщающий в себе среднюю величину затрат фирмы на одного сотрудника.

2.1.2.Эволюционным уравнением задачи является система уравнений (16) и (17), так как она удовлетворяет общему виду (П6) эволюционных уравнений:

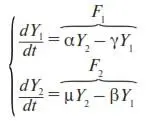
Применив к (18) условие (П8), найдем стационарное решение:

Y 1ст= Y 2ст= 0. (19)

2.1.3.Обратите внимание: наша модель средней фирмы имеет две переменные Y 1и Y 2. Следовательно, мы можем воспользоваться результатами Приложения П2.3, полученными для системы, так же с двумя переменными. В частности, чтобы проверить стационарное решение (19) на устойчивость, достаточно определить соотношение знаков у величин B , ∆ и D . Последние вычисляются по формулам (П22). В эти формулы входят четыре коэффициента линейного разложения: a 11, a 12, a 21и a 22. Их мы найдем с помощью (П12), в которой F i возьмем из системы эволюционных уравнений (18) нашей задачи.

Итак, согласно (П12),

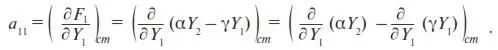
В первом слагаемом берется частная производная по переменной Y 1от выражения αY 2, которое, как видим, не содержит Y 1, поэтому, согласно правилу вычисления частной производной, это выражение считается постоянным и производная от нее равна нулю. Во втором слагаемом производная берется от выражения γY 1, которое считаться постоянным не может, так как содержит Y 1. Поэтому дальнейшие вычисления для a 11примут вид

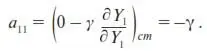
Аналогично рассуждая, находим остальные коэффициенты линейного разложения:

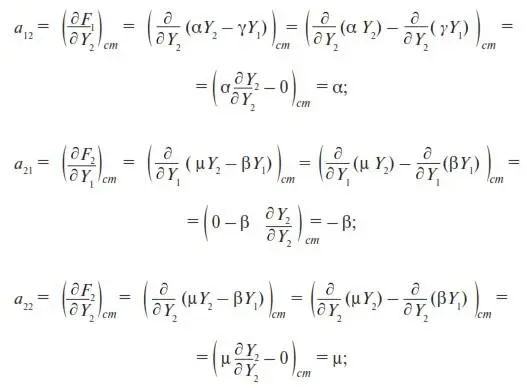
Подставив найденные значения a 11, a 12, a 21, и a 22в (П22), получим

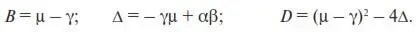(20)

2.1.4.Для средней фирмы коэффициенты α и β должны быть сравнительно большими, так как оба относятся к расходам на сотрудников, а коэффициент µ и γ , наоборот, не должен быть большими потому, что, во-первых (в случае µ ), у средней фирмы прибыль от операций на рынке не является слишком высокой, иначе бы фирма была богатой, а не средней; и во-вторых (в случае γ ), в цивилизованном обществе в средней фирме текучесть кадров невелика.

С учетом сказанного из формул (20) можно точно определить знаки величин ∆ и D . Действительно,

а) произведение больших коэффициентов α и β заведомо больше, чем произведение малых µ и γ , поэтому∆ > 0;

б) квадрат разности малых µ и γ есть очень маленькая величина, поэтому D < 0.

В отношении же B однозначного ответа нет: и µ , и γ – оба малые. Следовательно, мы приходим к двум возможным ситуациям: µ > γ и µ < γ .

Ситуация 1: µ > γ . Это означает, что коэффициент γ – невелик, и причин для увольнения мало.

В этой ситуации знаки величин из (20) распределятся следующим образом:

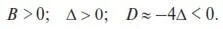
Такое сочетание знаков совпадает с (П30). В этом случае стационарное решение (19) соответствует неустойчивому фокусу. Фазовая траектория в координатах Y 1и Y 2представляет собой спираль, раскручивающуюся из начала координат (см. рис. П5).

Раскручивание спирали указывает на рост числа сотрудников Y 1и капитала Y 2. Но ввиду разновеликости коэффициентов β и µ ( β > µ ) наступает момент, когда во втором уравнении системы (18) в правой его части первое слагаемое окажется меньше второго и прирост капитала dY 2/dt станет отрицательным. На практике это выглядит так, что по мере роста числа сотрудников наступает момент, когда их становится настолько много, что фирма уже не может достойно (по мнению сотрудников) оплачивать их труд. Сотрудники увольняются. Последнее дает увеличение γ. И тогда фирма оказывается в ситуации 2.

Ситуация 2: µ < γ .

Соответствующее распределение знаков величин из (20) имеет вид