Игорь Дмитриев - Квантовая химия — ее прошлое и настоящее. Развитие электронных представлений о природе химической связи

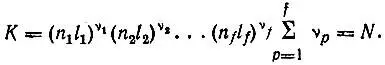(2.8)

Каждая (n рl р)-оболочка представляет набор 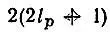спин-орбиталей, из которых ν pзаселены, т. е. включены в детерминант Слэтера. Эти ν pспин-орбитали можно выбрать из (n рl р)-оболочки 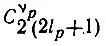способами. Следовательно, конфигурации К соответствует 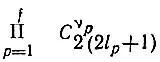однодетерминантных функций, причем их число определяется фактически лишь незамкнутыми оболочками, для которых ν p< 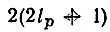. Например, для конфигурации ls 22s 22p 2атома углерода можно построить 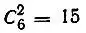детерминантов. Из них можно составить далее 15 линейных комбинаций, соответствующих определенным значениям квантовых чисел L и S и образующих атомные термы.

Термомназывается совокупность многоэлектронных функций определенной конфигурации, характеризующаяся общими для; всех функций терма значениями квантовых чисел полных орбитального и спинового моментов (L и S). Отдельные волновые функции терма различаются по квантовым числам проекций указанных моментов (M Lи M S). Если не принимать во внимание взаимодействие орбитального и спинового моментов, то все волновые функции терма отвечают одному и тому же (2L + 1)(2S + 1) — кратно вырожденному энергетическому уровню атома. Спин-орбитальное взаимодействие приводит к расщеплению этого вырожденного уровня на уровни тонкой структуры, характеризуемые квантовым числом полного спин-орбитального момента J. Поправка на спин-орбитальное взаимодействие определяется приближенным выражением

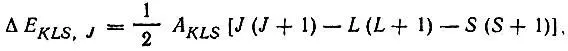(2.9)

из которого следует правило Ланде для константы спин-орбитального взаимодействия

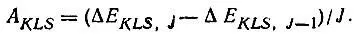(2.10)

Легко убедиться, что

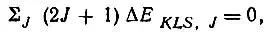(2.11)

т. е. энергия терма равна средневзвешенному значению энергетических уровней тонкой структуры:

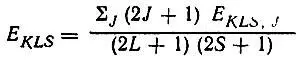(2.12)

Согласно правилам Хунда, энергия E KLS,Jбудет наименьшей, если: 1) квантовое число S максимально; 2) при равных S максимально квантовое число L; 3) при равных S и L квантовое число J максимально при A KLS<0 и минимально при A KLS> 0.

В качестве примера использования правил Хунда рассмотрим структуру энергетических уровней атома углерода для конфигурации ls 22s 22p 2(рис. 4). Из пятнадцати однодетерминантных шестиэлектронных функций этой конфигурации можно составить девять функций терма 3Р (L = 1 и S = 1), пять функций терма 1D (L = 2 и S = 0) и единственную функцию терма 1S (L = 0 и S = 0). Наименьшей энергии отвечает терм 3Р, обладающий максимальной мультиплетностью по спину. За ним следует терм 1D, поскольку он характеризуется большим значением квантового числа L, чем терм 1S, при равной спиновой мультиплетности.

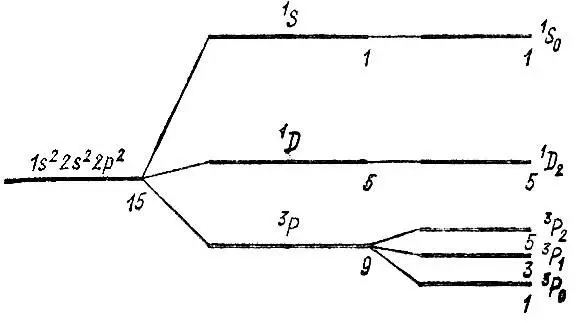
Рис. 4. Структура энергетических уровней атома углерода

Спин-орбитальное взаимодействие приводит к расщеплению лишь терма 3Р, так как для остальных термов полный спиновый момент равен нулю (а мультиплетность — единице). Для терма 3Р константа А > 0 и, следовательно, уровни тонкой структуры этого терма возрастают в последовательности 3Р 0, 3P 1, 3Р 2, где нижний индекс указывает значения квантового числа J.

Строго говоря, орбитальные энергии ε nl различны для разных термов одной конфигурации. Согласно расчету Клементи, атомным орбиталям 1s 22s 22p 2-конфигурации углерода в зависимости от терма соответствуют анергии ε nl (в атомных единицах):

Таким образом, расстояние между энергетическими уровнями 2s- и 2p-АО при переходе от терма 3Р к терму 1S увеличивается почти на 0,16 ат. ед., что соответствует 4,3 эВ или 98 ккал/ моль.

В большей степени орбитальные энергии зависят от атомной конфигурации. Эту зависимость можно показать на примере рассмотренной выше 1s 22s 22p 2-конфигурации и возбужденных 1s 22s 22p 3- и 1s 22р 4-конфигураций атома углерода [70]. Из множества термов, соответствующих этим конфигурациям, выберем термы 3Р и 1D:

Под полной электронной энергией атомной конфигурации следует понимать средневзвешенное значение энергии ее термов:

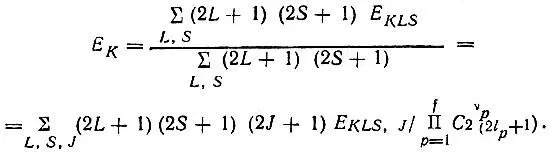(2.13)

Было бы ошибкой отождествлять энергию конфигурации с суммой орбитальных энергий

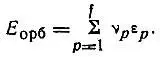(2.14)

Эта величина, как и орбитальные энергии, определяется не только конфигурацией, но и термом атомного состояния. Кроме того, E oрбсоставляет лишь часть, причем меньшую часть, полной электронной энергии термов.

По мере увеличения заряда атомного ядра погрешности, связанные с пренебрежением одноэлектронным спин-орбитальньм взаимодействием, увеличиваются, и приходится учитывать расщепление каждой ( nl )-оболочки на две подоболочки, различаю щиеся новым спин-орбитальным квантовым числом j :

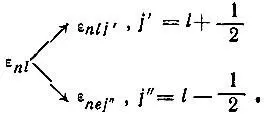
При этом атомные спин-орбитали уже не могут быть представлены как произведение орбитали и спиновой функции ( α или β ), и конфигурация атома характеризуется распределением электронов по ( nlj )-оболочкам: