Игорь Дмитриев - Квантовая химия — ее прошлое и настоящее. Развитие электронных представлений о природе химической связи
- Название:Квантовая химия — ее прошлое и настоящее. Развитие электронных представлений о природе химической связи
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:1980
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Игорь Дмитриев - Квантовая химия — ее прошлое и настоящее. Развитие электронных представлений о природе химической связи краткое содержание
Квантовая химия — ее прошлое и настоящее. Развитие электронных представлений о природе химической связи - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
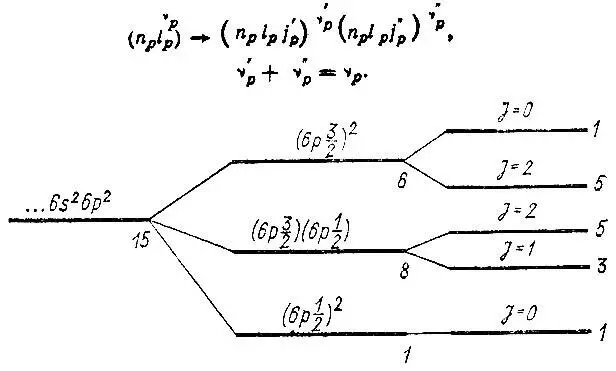
Рис. 5. Структура энергетических уровней атома свинца
Многоэлектронные волновые функции, соответствующие уровням тонкой структуры, строятся в этом приближении, называемом приближением j-j -связи, непосредственно из детерминантов "расщепленной" конфигурации.
Схему j-j -связи иллюстрирует пример атома свинца, основная конфигурация которого (...6s 26p 2) аналогична основной конфигурации атома углерода (...2s 22p 2), но существенно отличается от последней структурой энергетических уровней (рис. 5)
Следует подчеркнуть, что выбор квантовых чисел, определяющих состояние атома, зависит от того, в каком приближении мы его рассматриваем. Так, без учета спин-орбитального взаимодействия состояние атома характеризуется квантовыми числами L и S. Однако при учете этого взаимодействия уже нельзя говорить о сохранении орбитального и спинового моментов по отдельности, и соответствующие им квантовые числа L и S не будут более "хорошими" квантовыми числами. Вместо них следует использовать квантовое число J, характеризующее полный спин-орбитальный момент импульса, который в этом приближении будет сохраняться. В то же время если спин-орбитальное расщепление энергетических уровней достаточно мало, можно установить соответствие между уровнями тонкой структуры и определяемыми в более грубом приближении энергетическими уровнями термов. Точно так же для тяжелых атомов квантовое число l , характеризующее одноэлектронный орбитальный момент импульса, перестает служить "хорошим" квантовым числом, лишь только мы учитываем спин-орбитальное взаимодействие на одноэлектронном уровне.
Атомные орбитали и их графическое представление
Рассмотрим атом водорода — простейший из атомов, включающий лишь один электрон, который взаимодействует с ядром по закону Кулона. Задача определения электронных состояний атома водорода (квантовомеханическая проблема Кеплера) — одна из немногих задач квантовой механики, имеющих точное аналитическое решение. Такая возможность обусловлена тем, что в этом случае гамильтониан допускает разделение переменных в сферической системе координат (r, υ, φ), т. е. орбиталь ψ, описывающая движение электрона в поле ядра, может быть представлена в виде произведения трех функций и каждая из них зависит только от одной независимой переменной:
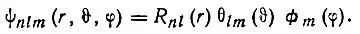 (2.15)
(2.15)
При этом орбиталь ψ nlm характеризуется тремя квантовыми числами: n, l и m (табл. 1).

Таблица 1. Атомные орбитали атома водорода для n = 1, 2, 3
Квантовое число l , целое и неотрицательное, определяет орбитальный момент импульса электрона, точнее его квадрат: l(l + 1).
Квантовое число m , целое и не превышающее по абсолютной величине l , представляет проекцию орбитального момента импульса на произвольно выбранную ось квантования z .
Главное квантовое число n нумерует орбитальную энергию ε n в порядке возрастания:
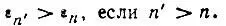 (2.16)
(2.16)
Характерным для атома водорода является то, что энергия ε n не зависит от квантового числа орбитального момента импульcа и определяется главным квантовым числом n :
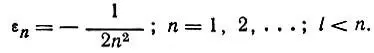 (2.17)
(2.17)
Для многоэлектронных атомов проблема усложняется. Хотя одноэлектронное приближение и сферическая модель самосогласованного поля позволяют произвести разделение переменных r, υ, φ и в этом случае, точное аналитическое выражение для радиальных функций R(r), к сожалению, не получается. Они определяются в приближении самосогласованного поля решением уравнений Хартри-Фока (см. гл. 3). Соответствующие орбитальные энергии ε nl зависят как от главного, так и от орбитального квантовых чисел, причем главное квантовое число n нумерует ε nl с фиксированным l в порядке возрастания целыми числами, начиная с (l + 1).
Радиальная зависимость орбиталей в многоэлектронных атомах может быть довольно сложной, но их узловая структура подобна узловой структуре орбиталей атома водорода: радиальная функция R nl (r) характеризуется (n-l-1) узлом, т. е. обращается в нуль при (n-l-1) конечном значении r > 0.
Графическое представление радиальных функций.Для графического представления радиальных функций используется либо график самой функции R nl(r), либо график соответствующей ей плотности вероятности локализации электрона на расстоянии r от атомного ядра:
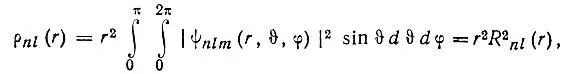 (2.18)
(2.18)
причем функция ρ nl(r) нормирована на единицу:
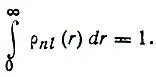 (2.19)
(2.19)
Следует отметить, что в соответствии с условием формировки сферических функций интегрирование по углам υ и φ не приводит к появлению множителя 4π, который иногда ошибочно включается в выражение для ρ nl(r).
Примеры графического представления радиальных функций приведены на рис. 6.
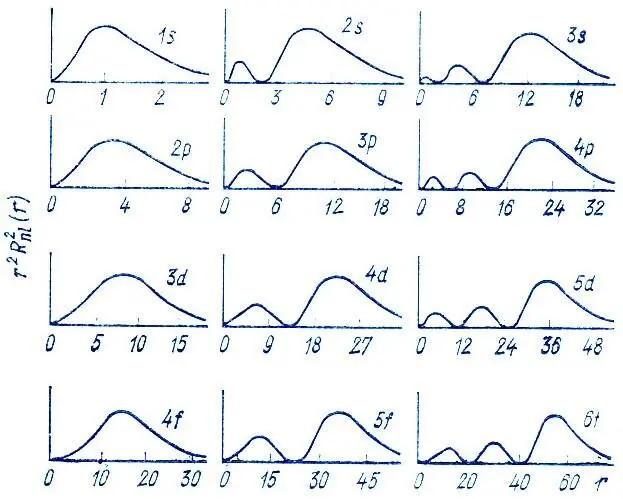
Рис. 6. Графическое представление радиальных функций
Графическое представление угловой зависимости атомных орбиталей.Для графического представления сферических функций
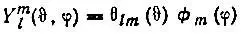 (2.20)
(2.20)
используются полярные диаграммы, т. е. графики функций
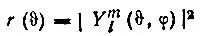 (2.21)
(2.21)
в сферической системе координат.
Полярная диаграмма описывает распределение вероятности локализации электрона по направлениям, заданным углами υ и φ. Легко видеть, что полярные диаграммы аксиально симметричны, если атомные орбитали характеризуются определенными значениями квантового числа m , т. к. в этом случае их зависимость от угла должна иметь вид
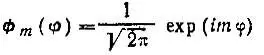
Интервал:
Закладка:









